普通の人が資産運用で99点をとる方法とその考え方
2024年9月13日、「普通の人が資産運用で99点をとる方法とその考え方」が日経BPから出版されました。詳しくはこちら。
はじめに
資産運用で 99 点をとる方法とその考え方について説明します。この記事の対象はいわゆる「普通の人」です。
- 資産運用は趣味ではない。
- 資産運用を始めてみたいが何をしてよいのかわからない。
- 資産運用をすでに行っているが毎年ころころと方針を変えてしまっている。
- 資産運用に無駄に時間ばかり費やしている。
- 今のところ資産はすべて銀行の普通口座や定期預金にいれている。このまますべて現金でおいておくのも何か損しているみたいでモヤモヤする。だけど難しいことは勉強したくないし時間も使いたくない。
といった人たちです。
記事では最初に結論、すなわち「やるべきこと」を述べます。資産運用で 99 点の投資効率を達成するためにはこの結論部分だけを実行するだけでよいです。
次に、それだけでどうして 99 点といえるのか、その裏付けとなる考え方や理論を中心に説明します。 99 点をとるにあたってこれらの知識を勉強する必要はありません。しかし、われわれ「普通の人」にとっては最初に決めた方針を貫くこと、別の言い方をしますと「余計なことをしないこと」が難しかったりします。この理論編は方針を継続する支えとなる知識を身につけるためにあります。
最後に、いくつかの資産運用についてよくある質問とその答えをまとめています。
今後もこの記事の内容は必要に応じてアップデートする予定です。ただし、基本となる考え方は本質的でありこれからも変わることはないでしょう。
記事の内容に Typo や間違いを発見した場合、コメント・質問等がある場合は、GitHub Issues に報告や質問をお願いします。記事に載せたほうがよい質問があった場合は、適宜この記事に追加します。
最後にお約束ですが「投資は自己責任」です。この記事はあくまで筆者の考え方をまとめたメモと考えていただければ幸いです。
更新履歴
直接、ここ (Blame の結果)をみてもらうのが一番早いです。以下の更新履歴はおまけ程度です。
- [2024-10-23 Wed] 目次を追加。内容は同じ。
- [2024-08-01 Thu] Editorial change.
- [2023-11-12 Sun] 構成を変更するとともに、結構な箇所を加筆。
- [2023-01-08 Sun] FAQ: 「特定口座から新 NISA に移したほうがよいでしょうか?」を追加 (Issue #55)。
- [2023-01-08 Sun] 新 NISA に対応。
- [2021-03-02 Tue] この記事は 2020 年「はてなブックマーク年間ランキング」で一位になりました。
- [2020-12-07 Mon] 現金 100%のアセットアロケーションを追加。
- [2020-05-06 Wed] FAQ: 「インデックスに加えて個別株にも手を出しています。いけないでしょうか?」を追加。
- [2020-01-24 Fri] 最適なポートフォリオを個人で組もうとする行為がいかに無駄かについて加筆。
- [2020-01-23 Thu] ドルコスト平均法について加筆。
- [2020-01-23 Thu] いただいた質問(出口戦略・高配当株について)と答えについて追加。
- [2020-01-12 Sun] 中央値について加筆。中央値の良さを表す式を追加。
- [2020-01-07 Tue] Fix Typo ( Issue #32, Issue #33, PR #34, PR #35)
- [2020-01-05 Sun] Fix Typo (25,00 円 => 25,000 円) (via PR #26), PR #28, PR #31, スタイル修正 (PR #29, PR #30)
- [2020-01-05 Sun] お得度を「点数」ではなく「相対的な数字」と表記
- [2020-01-05 Sun] Fix Typo (債権 => 債券)。
- [2020-01-04 Sat] 公開
結論編
結論
結論だけ最初に教えてください。資産運用を始めてみたいのですが何をしたらよいのでしょうか?
以下のことだけをしましょう。これだけで投資効率が 99 点になります。
- 確定拠出年金 (iDeCo または 企業型 DC)を始めます。
- 新 NISA でつみたての設定をします。
- さらに余裕がある方は、特定口座でつみたての設定をします。
- 資産運用を始めた直後や、まとまった資金を一時的に入手したときなど、十分な余剰資金(現金)をもっているのであれば、自分のリスク許容度の範囲内で、適切な割合の資産を 一括 で投資します。詳しくは後述の「アセットアロケーション」を参照してください。
- 定期的に(年に 1 回、あるいは数年に 1 回)、アセットアロケーションについて見直しましょう。
1, 2, 3 は一度設定するだけです。 4 は資産運用を始めるとき、あるいは、まとまった資金を贈与されたときなど一時的に行うものです。
この方針をちゃんと守っているならば資産運用に使用する時間は 1 年に 30 分もないはずです。
1, 2, 3, 4 において購入するべきものはすべて同じものでかまいません。以下の条件:
- コスト(信託報酬)の安い
- 時価総額加重平均を採用したインデックスファンド (S&P500、全米、全世界など)
を満たすものにしましょう。これらの条件を満たすものは:
- eMAXIS Slim 全世界株式 (オール・カントリー)(通称: オルカン)
- eMAXIS Slim 米国株式 (S&P500)
- SBI・V・S&P500 インデックスファンド
などです。これらはネット証券 (SBI 証券、楽天証券など)で購入します。
注意) 新 NISA は「つみたて投資枠(上限: 年間: 120 万円)」と「成長投資枠(上限: 年間 240 万円)」に分かれていますがその名前に惑わされて別のものを買う必要はありません。この記事内の「新 NISA」は両者を特に区別しません。単に年間の上限枠が 360 万円である非課税枠として扱います。
具体的な手順(証券会社の口座の開設や設定方法など)はこの記事では説明しません。この記事では方針とその考え方のみ述べます。
してはいけないこと
してはいけないことは何でしょうか?
資産運用において大事なのは「余計なことをしない」ということです。例えば、以下のことはしてはいけません。
-
「マーケットタイミング」を計る
例)
- 「今は株価が高値だから、現金をためておこう。暴落したら一挙に購入しよう」
- 「暴落の噂があるからいまのうちに売却して利益確定しておこう」
-
時価総額加重平均インデックスではないファンドや個別株を購入する
例)
- XXX 社の株を買う。「AI 関連ファンド」等を購入する。高配当株を購入する。
-
怪しいもの・実績がないものに手をだす
例)
- 記事の公開にあたってこの部分は削除しました。具体的に書くと怒られそうなので ...察してください。
これらはすべて投資効率を下げる行為です。99 点から点数がどんどん下がっていくと考えてください。そもそもこれらは「選択・判断」しないといけないため、自分の時間がとられてしまいます。
もし、自分が:
- 1 年に 30 分以上資産運用に時間を使っている
- あるいは、1 年に 1 回以上最初の方針にはなかった「投資判断」を行っている
のであれば、それは最初の方針を曲げてしまっている、何かが間違っている証拠です。長期的にはその「ツケ」は必ず払わされるでしょう。
幸いなことに、われわれは「普通の人」であり資産運用は趣味でもエンタメでもありません。そのことが逆にアドバンテージになると考えるとよいでしょう。
枠のお得度
「1. iDeCo」「2. 新 NISA 」「3. 特定口座」 のうちどれを優先するべきですか?
それぞれのお得度をあえて「雑」に相対的な数字で表現するならば:
| 枠 | お得度 |
|---|---|
| 1. iDeCo (上限あり) | 140 |
| 2. 新 NISA (上限: 毎年 360 万円, 合計 1,800 万円) | 120 |
| 3. 特定口座でインデックスファンド | 100 |
と考えましょう。お得度の高いものから順番に使いきるようにしましょう。
ただし、注意点として iDeCo については 「資金拘束」、すなわち 60 歳 (or 65 歳) になるまでは引き出すことができないという制限があります。 iDeCo についてはこの条件がクリアできる範囲で拠出しましょう。
iDeCo のお得度は実際にはさまざまな条件によって異なってきます。あまり細かいことはここでは述べませんが、iDeCo の最大のメリットは所得控除です。所得にかかる税金が軽減されるということは、その分資産運用の額を増やせる・ その結果増やした資産運用額が複利をさらに生み出します。運用期間や種々の条件にもよりますが、この効果は一般的には NISA の非課税効果(利益の 20%)よりも大きいです。
iDeCo は受取時に税金がかかりますが、ほとんどのケースにおいては退職金控除等の効果が大きく支払う税金は比較して安くなるでしょう。
仮に支払う税金額が同じになるとした場合でも iDeCo を利用した場合は「税金の支払いを未来に先送りすることができる」と考えることができ、それは先程述べたような効果を生みます。
「今 1 万円を支払う」のと「30 年後に1万円を支払う」のでは、後者のほうが「お得」です。
例
A さんは年間 50 万円投資に資金を回せます。A さんは iDeCo は使用しないとします。
このとき:
- 「今年は新 NISA で 20 万円分、特定口座で 30 万円分、購入しました。」
よりは
- 「今年は新 NISA で 50 万円分、購入しました。」
のほうがよいです。なぜなら、前者は新 NISA の枠を使い切っていないのに、特定口座で商品を購入しているからです。後者のようにまずは(可能なら)新 NISA の枠を使い切りましょう。
アセットアロケーション
資産のうちどれだけの割合をリスク資産に回せばよいのでしょうか?
アセットアロケーションを決めるのは、主に次の 2 段階で行います。
- 投資効率(いわゆるシャープレシオ)のもっともよいリスク資産を選択する。
- 個人のリスク許容度(あるいはリスク選好)に応じて、安全資産である現金と 1 で選んだリスク資産の割合を決定する。
幸いなことに今は 1 については悩む必要はありません。先ほど示した時価総額加重平均にもとづくインデックスファンド 1 択です。商品によって多少のコスト差はありますがもはや誤差の範囲内といってよいでしょう。理論的には「誰でも同じ選択」になります。
個人によって変わるのは、2 の部分です。
例: アセットアロケーション
資産の合計が 1,000 万円だとした場合、リスク許容度に応じたアセットアロケーションの目安は以下のようになります。
| リスク許容度 | 現金:リスク資産 | 現金 | リスク資産 | 全体のリターン | 全体のリスク |
|---|---|---|---|---|---|
| 資産が 50%減る (= 500 万円になる) ことを許容できる | 0:100 | 0 万円 (必要最小限なものは除く) | 1,000 万円 | 5% | 10% |
| 資産が 25%減る (= 750 万円になる) ことを許容できる | 50:50 | 500 万円 | 500 万円 | 2.5% | 5% |
| 資産が 10%減る (= 900 万円になる) ことを許容できる | 80:20 | 800 万円 | 200 万円 | 1% | 2% |
| 1 円たりとも損するのは絶対に許せない | 100:0 | 1,000 万円 | 0 万円 | (ほぼ) 0% | 0% |
- リスク資産とは (iDeCo + 新 NISA + 特定口座) の合計です。
- リスク資産の最大損失額として、ここでは-50%と仮定しています。これは相当(安全側に倒した)「悲観的」な見積もりです。一般にはもう少し「楽観的」な数字(-33% など), あるいはリスクの 3 倍(= 1%以下の確率)を用いますが、われわれ「普通の人」は、慣れるまでは -50%(およそ半額になる)くらいと見ておけば十分でしょう。ただし、必要以上に保守的にならないでください。
- ここでは仮にリスク資産のリターンを 5%、リスクを 10%としています。
- 現金とリスク資産の間には相関関係はないので、現金比率をいくつにしようと、アセットアロケーション全体のシャープレシオ (= (リターン / リスク)) は変わりません。どのようなアセットアロケーションにしようと、全体のシャープレシオは、1 で選んだもっとも投資効率のよいリスク資産のシャープレシオと一致します(ただし現金 100% のアセットアロケーションは除く)。現金(無リスク資産)のリターンはゼロとしています。
- アセットアロケーションによって、全体のリスクとリターンが決まるため、資産運用のパフォーマンスは結局のところ「アセットアロケーション x 資産運用の年数」でほぼ決定されます。
資産運用とは、結局のところ、アセットアロケーションにおいて、現金とリスク資産の比率を適切な値に調整しましょうということです。それでほぼすべてが説明できます。それ以外はすべてそのための手段にすぎません。
イメージとしては、このようなスライダー:
現金 リスク資産
のバーを本人のリスク許容度から大きくずれたりしないように調整するというのが資産運用です。
いわゆる「つみたて」も、あくまでこのスライダーのバーが時間の経過とともにいつのまにか大きくずれている、現金の割合が多くなっていく、のを防ぐためのもの、と考えればよいでしょう。
インデックスファンドは流動性が高い資産です。現金とリスク資産は、必要に応じていつでもすぐに(ほぼ数日で)変換可能です。つまり、現金が予想以上に必要になったときは、リスク資産の一部を売却すればよいだけの話です。
資産運用とは決して「節約しよう!」という意味ではないです。「節約」と「運用」は分けて考えるべきです。例えばフルインベストメントしている人が、予想以上に現金が必要になったときは、必要なぶんだけリスク資産の一部を売却すればよいです。そこは躊躇する必要はまったくありません。必要なときはどんどんお金は使いましょう。資産運用とは、あくまで資産のうち「適切な割合」をリスク資産にしておくということです。
参考) Two-Fund Separation Theorem and Applicationsk, Two-fund separation - Individual decision
資産運用の実践例
例: A さんの場合
A さんは社会人 8 年目です。今まで資産運用はまったくしてきませんでした。 A さんの資産は銀行口座に 400 万円です。
現金 リスク資産
- A さんは、現在の資産 400 万円のうち 4 分の 1 (= 100 万円) 資産が減っても、十分許容できると考えました。つまり、アセットアロケーションは 現金:リスク資産 = 50:50 にすると決めました。
- A さんは、現在 400 万円ある現金のうち、50%である 200 万円を一括で投資しました。すべて新 NISA の枠を使用しました。
現金 リスク資産
A さんの今の手取りは 40 万円です。A さんは生活費として 24 万円使用します。つまり毎月 16 万円貯金できます。
- A さんは毎月貯金していた 16 万円のうち、50%である 8 万円を資産運用に回すことにしました。
- A さんは iDeCo をはじめました。月々の拠出額は最大の 23,000 円です。
- A さんは 新 NISA で 毎月 57,000 円 のつみたてを設定しました。先程一括で投資した分とあわせても 年間の合計は 200 + 5.7 x 12 = 268 万円であり、これは 新 NISA の年あたりの枠の上限 360 万円に収まります。
A さんがやるべきことはこれで終了です。あとは、定期的にアセットアロケーションを見直すだけでよいでしょう。
例: B さんの場合
B さんは社会人 2 年目です。今まで資産運用はまったくしてきませんでした。 B さんの資産は銀行口座に 100 万円です。
現金 リスク資産
- B さんは、現在の資産 100 万円のうち 半分(= 50 万円) 資産が減っても、十分許容できると考えました。つまり、アセットアロケーションは 現金:リスク資産 = 0:100 にすると決めました。いわゆるフルインベストメントです。
- B さんは、現在 100 万円ある現金のうち、最低限残しておく部分は除いて、ほぼすべてを一括で投資しました。すべて新 NISA の枠を使用しました。
現金 リスク資産
B さんの今の手取りは 20 万円です。B さんは生活費として 15 万円使用します。つまり毎月 5 万円貯金できます。
- B さんは iDeCo をはじめました。月々の拠出額は最大の 23,000 円です。
- B さんは 新 NISA で 毎月 27,000 円 のつみたてを設定しました。
B さんがやるべきことはこれで終了です。あとは、定期的にアセットアロケーションを見直すだけでよいでしょう。
例: C さんの場合
C さんはすでにリタイアしており年金で生活しています。C さんの資産は現在 1,500 万です。 今まで投資とは縁のなかった C さんですが、将来の生活にやや不安を感じており、新 NISA の話を聞いたのがきっかけで投資について興味を持ちました。何事も遅すぎるということはない、やらないよりはましだと思い、 C さんは投資を始めることにしました。
現金 リスク資産
- C さんは iDeCo はできませんので、新 NISA をはじめることにしました。
- C さんは年金があるため 1500 万円のうち半分を投資にまわしても当面の生活に支障はないと考えました。
- C さんは 新 NISA で毎月 30 万円 のつみたてを設定しました。新 NISA は一年あたり 360 万円までなのでこれで年間の枠を使いきります。
- C さんは残りの投資可能額、約 400 万円を来年の新 NISA の枠で投資する予定です。それまでの間 400 万円は特定口座で運用することにしました。来年、様子を見て、特定口座から新 NISA に移す予定です。
現金 リスク資産
C さんがやるべきことはこれで終了です。来年以降、C さんは必要に応じて新 NISA の枠を最優先で使用すればよいでしょう。いずれ特定口座は使用しなくなり、リスク資産はすべてを新 NISA で運用することになるでしょう。
C さんのようなケースに対しては「投資を始めるの遅すぎ」「もう手遅れでしょ」という意見が通常は多く見られると思います。ですがそのような意見は投資に興味をもった・投資を始めたいと思っている C さんにとって余計なお世話でしょう。資産運用の期間は長ければ長いほどよいというだけであり、「40 年以上資産運用しないと意味がない」というものではありません。なにもしないよりは 1 年運用したほうがよい、1 年よりは 2 年のほうがよい、2 年よりは 3 年のほうがよい...というだけの話です。投資を始めるにあたって始めるときの年齢や資産額を気にする必要はありません。
余計なことはしない
ほんとにやるべきことはたったそれだけでいいのですか?早い話が一度設定した後は、「何もしなくてよい」ということでしょうか?
はい。一度設定した後は基本放ったらかしにしましょう。資産運用に時間を使う必要はありません。一度設定したあとは定期的に、あるいは何かライフイベントがあったときに、アセットアロケーションを見直せばよいでしょう。
これで結論編はおわりです。この通りにきちんと実行できる、あるいはもうすでに実行できているという人は、これ以上、この記事を読まなくても大丈夫です。ここから先はある意味すべて蛇足です。
理論編
次に理論編です。先程の結論で示した方針を実行するのは簡単そうに聞こえます。ですが、この世の中にはその妨げになる「情報」がたくさんあふれています。
- 「いま、株価は史上最高値です! PER は過去最高です!暴落は 2 年以内におとずれるでしょう!」
- 「暴落はまだ始まったばかりです。これから株価はもっと下げます。全部、現金にしましょう!」
- 「インデックス投資なんて大して儲かりませんよ!短期間で大儲けするなら、FX です!」
- 「仮想通貨で 1 億円儲かりました!」
- 「XXX 社の株が狙い目です!確実に儲かりますよ!」
- 「これからは AI の時代です。AI 関連の会社の株を買うのがおすすめです!」
などですね。我々のような「普通の人」は普通の耐性しか備えていないので、これらの雑音や誘惑に対抗できずに、どんどんダークサイドに落ちていくことでしょう。
考え方や理論を学ぶ重要性はここにあります。人間の感情を巧みについてくるこれらの情報への対抗力を身につけるために、知識武装をするのです。
「インデックスファンドをひたすら買うだけで 99 点を達成」できるにもかかわらず、多くの人が(本人にはその気がないのかもしれませんが)「もっとよい成績をとってやろう」といつの間にか思ってしまい、余計なことをしてしまい、その結果、投資効率が 99 点からどんどん落ちていくのです。
市場平均
最適なポートフォリオは市場平均 / 基本となる考え方
ここでは要点だけ述べます。
- 株価はランダムウォークしながらも長期的には右肩上がりだという前提にたちます。
- インデックスファンドは株式市場をまるごと買う行為です。まるごと買うとは、一切のバイアス・私見をいれずに、ありのまま時価総額に応じてすべてを保有することです。つまり、インデックスファンドをひたすら買うことで、資産運用の成績は、時価総額加重平均・いわゆる市場平均とほぼ同じになります。詳しくは後述。
- すべての情報は市場に織り込み済みです。いわゆる市場は効率的であるという前提にたちます。完全に効率的かというとそうではないでしょうが、少なくとも、個人投資家が継続的に利益を得られるほどの非効率性はないという意味で、十分に効率的と考えるべきです。
- つまり、すべての情報を織り込んだ・市場全体の総意によって決定されている株価はいつだって「適正価格」です。「今の株価は高値圏」「今の株価は安値圏」「そろそろ暴落が来そう」などといった分析・情報はまったく無意味と思いましょう。株価は見る必要はありませんし予想する必要もありません。株の買い時・売り時はありません。あえて言うなら、365 日 24 時間、いつだって(リスク許容度の範囲内で)「買い時」と仮定しましょう。
- 市場平均に勝とうとすればするほど、余計なコストがかかり、長期的には市場平均に負けていきます。
- 長期的に市場平均に勝てる個人投資家はほぼいません。40 年くらいの期間だと、市場平均に勝てる人は、50 人に 1 人くらいはいるかもしれませんが、われわれ「普通の人」がその 1 人であると信じる根拠にどこにもないです。
- つまり、個人投資家が長期でとれる最大の成績は「市場平均」です。
参考) 敗者のゲーム
市場平均ってなんか言葉が弱そうなんですけど。ほんとに市場平均を目指すだけでいいんですか?もっと上を目指さなくてよいのでしょうか?
はい。
- 株式市場の取引のほとんどは「機関投資家」というプロ中のプロにより行われています。
- 市場平均というのは、プロ中のプロである巨大な専門機関のトップクラスたちの成績の平均ということです。
- われわれが株を買うときその裏で株を売っている相手は巨大な専門機関のトップクラスであり、われわれが株を売るときその裏で株を買っている相手もプロです。
- 市場平均に勝とうというのは、われわれ「普通の人」が、情報も頭脳も分析力もすべてにおいて優れているプロ中のプロに勝とうとする行為です。
- ちなみに機関投資家自身も市場平均には勝てません。なぜなら、市場平均というのは彼ら自身だからです。自分は自分には勝てません。
- そのような知識も経験も分析力も圧倒的に劣るわれわれ「普通の人」が、プロ中のプロである彼らの成績の平均をとる方法があります。それが「株式市場をまるごと」買うということです。インデックスファンドはそれを可能にします。
つまり、インデックス投資とは、プロ中のプロがだした結果の平均である「市場平均」を、なんの努力もしない、勉強をしないで、(言葉は悪いですが)美味しいところだけいただくということです。
インデックスファンドをひたすら買うだけで、あなたは「普通の人」ではなく、「プロ中のプロの平均」になります。
この際、決して「市場平均よりよい成績をとってやろう」と「勝手な行動」をとらないでください。その瞬間、魔法がとけて、あなたはただの「普通の人」になってしまいます。ただの「普通の人」の投資判断が、長期で継続的に市場平均に勝てることはないでしょう。
参考) 敗者のゲーム
99点
さきほどから 99 点といっていますが、その点数はどういう意味でしょうか?
仮に以下のような理想的なあなた専属の運用ロボットがいるとして:
- 基本的な資産運用方針はあなたとまったく同じ。
- あなたのリスク許容度を完璧に理解している。
- ただし、手間を惜しまずできるだけ早くあなたの資産をあなたの代わりに投資に回してくれる。例) 「毎月つみたて」のような特定の日を待たずに、手動でタイムリーに購入。
- アセットアロケーションのリバランスも、リバランスのコストよりもリバランスのメリットがある限り頻繁に行う。手間をまったく惜しまない。
この理想的なロボットに運用をまかせたときの成績を X とした場合、だいたい
0.99 * X くらいの成績を手間をかけることなくとりましょう、という意味です。
つまり、手間をかければかけるほど理想的な 100 点に近づくことはできますが、99 点を 100 点にするのはその手間を考えたら割にあわない。手間なしで 99 点で十分です。
時価総額加重平均
どうして時価総額加重平均にもとづくインデックスファンドが良いのでしょうか?なにか理論的な裏付けがあるのでしょうか?
理論的な裏付けがあります。時価総額加重平均インデックスにもとづくポートフォリオ(= 市場ポートフォリオ: Market Portfolio) がもっとも投資効率がよいポートフォリオ (= tangency portfolio)と、理論上はされています。
理論がどこまでの精度で当てはまるのかはわかりませんが、少なくとも「普通の人」がそれを否定して他のポートフォリオを選択する理由はないでしょう。
以下は証明にはなっていませんが、直感的に「なんとなく納得」するには、これで十分でしょう。
- 株の需要と供給は一致する
- 最適な組み合わせがあると仮定し、それを A とする
- 個々の投資家は最適な組み合わせである A を選択しようとする
この場合、市場に存在する各銘柄の時価総額と、全投資家が保有するの株の価値の合計額が一致するのは、A が時価総額加重平均である場合のみです。
参考) Two-fund separation - Market level, Capital market equilibrium - The Capital Asset Pricing Model
平均という言葉の罠
「市場平均」とは一般には「時価総額加重平均ポートフォリオ」あるいは「その成績」のことを意味します。ですので、先程のように「市場平均」のことを「投資家の間の平均点」と称するのは、正確な表現ではなく誤解を招く表現です。実際には、「市場平均」は単なる「みんなの点数を足して人数でわった平均点」ではなくて「株式市場でとれる理想的な平均点」です。「市場平均」を取り続けることは長期になればなるほど優位に働きます。「市場平均」の「平均」という言葉のイメージから、「たんなる平均点でしょ? 1 年 2 組の数学のテストの平均点のようなものでしょ?それなら平均点を上回る人は半分くらいいるってことでしょ?」と考えてしまいがちですが、これは「平均」という言葉がもたらすイメージの罠です。実際には「市場平均」とは「もっとも最適な成績」です。株式にリスクがある以上、毎年一番の成績をとるわけではないですが「長期的にはクラスで一番の成績をとる人」というイメージでとらえたほうが正確です。
リスクをきちんと理解する
長期で資産運用するのであれば、結果は期待リターン(平均値)に収束していくんだから、リスクは気にしなくてよいのでは?リターンだけ追求すればよいのでは?
いいえ、違います。リスクは資産運用の敵です。リスクは「平均値」(期待リターン)には影響は与えませんが、「中央値」(上位 50%の成績)に影響を与えます。
これは実際に成績の分布を見るのがわかりやすいでしょう。たとえば、以下のような 2 つのファンドがあるとします。
| リターン | リスク | |
|---|---|---|
| A | 5% | 5% |
| B | 5% | 20% |
A、B どちらもリターンは同じ 5%ですが、A の方はリスクが 5%、B の方はリスクが 20% です。A, B をそれぞれ 10 年間投資した場合の成績を見てみましょう。
実際はこのような A, B が両方存在することはないです。なぜなら、全員 A を選択するからです。B は誰からも選ばれません。
リターンの分布 (x 軸: 成績, y 軸: 確率密度)
A) リターン 5%, リスク 5% の場合: (html)
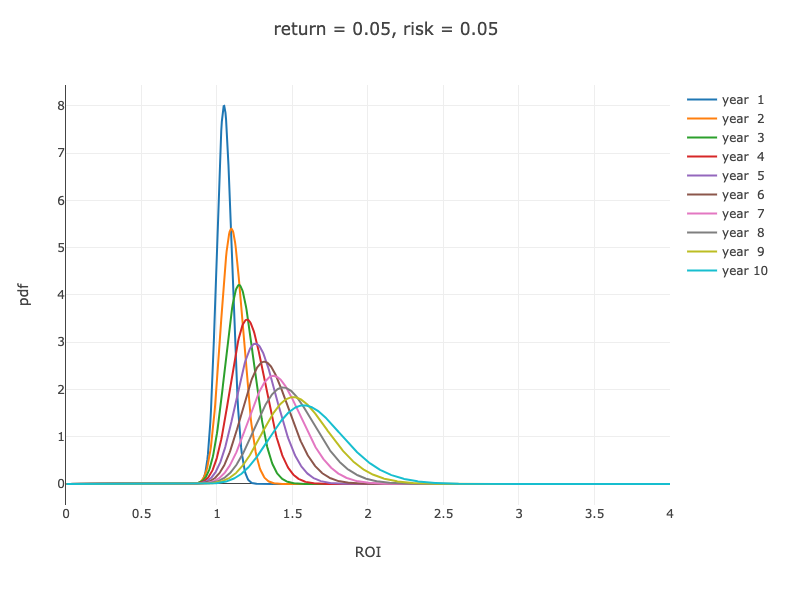
B) リターン 5%, リスク 20% の場合: (html)
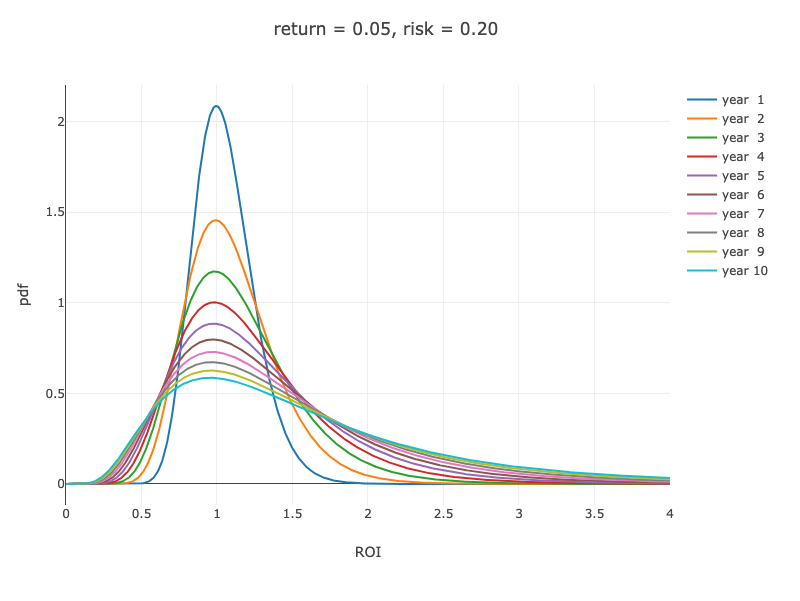
- A と B を比較した場合、成績の分布の形はずいぶん異なります。B のほうが A よりも分布は「左側に集中」していますが、いずれも期待リターンは同じになります。たとえば 10 年後の期待リターンはどちらも 1.629 (= $ 1.05^{10} $) です。
- 一般に成績の分布は、左に偏った、右側に長く伸びるロングテールになります。リスクが高ければ高いほどその傾向がつよくなります。
- リスクが高ければ高いほど、多くの人が左側に偏ってしまう一方、一部の成績のいい「ラッキー」な人は分布上ではいくらでも右側に伸び続けます。
- 期待リターンはそれらの一部の「とてもいい成績をとっている人」の影響が強くなります。実際にはそのような「大儲け」できる人はほとんどいないにもかかわらず、です。
- リスクがある限り、期待リターンを達成できる人は常に 5 割を下回ります。リスクが大きくなれば大きくなるほど、期待リターンを達成できる確率は小さくなります。中央値(上位 50%の人の成績)は期待リターンを常に下回ります。
期待リターン(mean), 中央値(median; μ)、中央値 ± 標準偏差 (x1, x2) のチャート (x 軸: 年数, y 軸: 成績 (対数))
A) リターン 5%, リスク 5% の場合: (html)
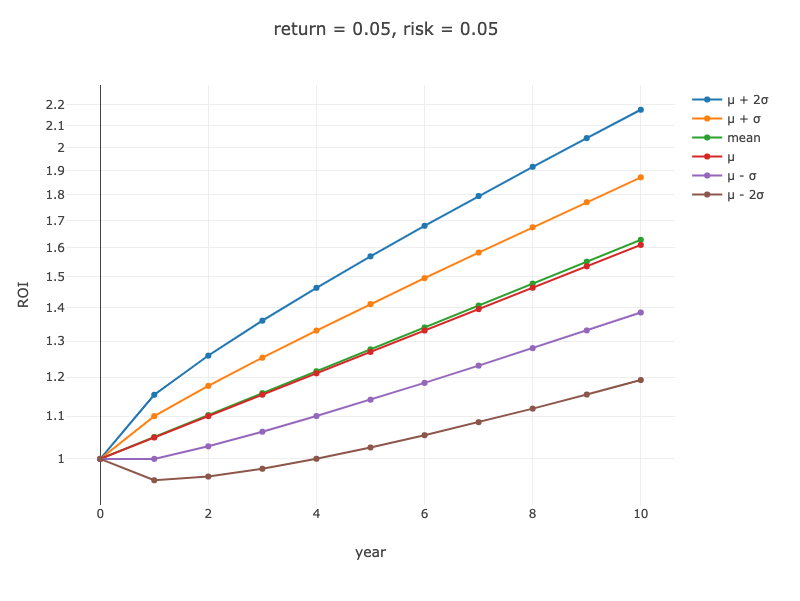
B) リターン 5%, リスク 20% の場合: (html)
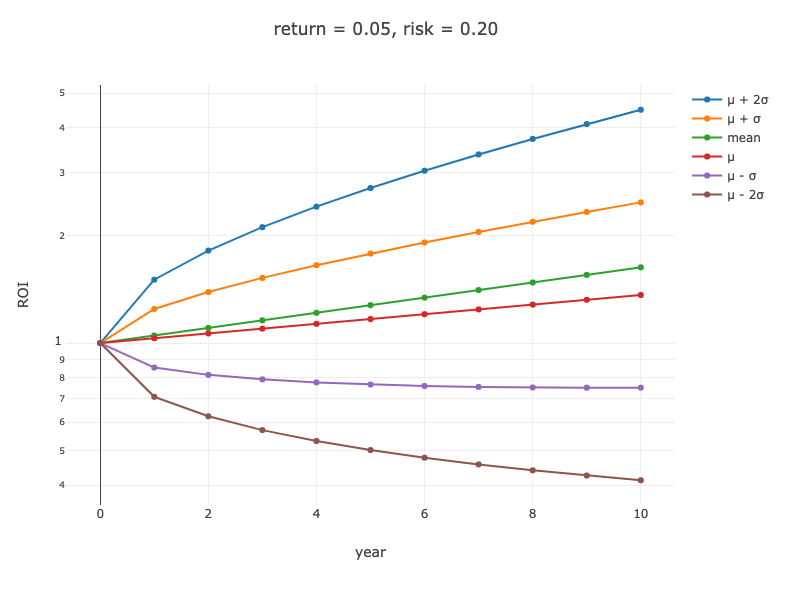
| percentile | A (risk: 5%) | B (risk: 20%) |
|---|---|---|
| μ + 2σ (97%) | 2.176 | 4.498 |
| μ + σ (84%) | 1.874 | 2.476 |
| mean (期待リターン) | 1.629 | 1.629 |
| 中央値: μ (50%) | 1.611 | 1.363 |
| μ - σ (16%) | 1.386 | 0.750 |
| μ - 2σ (2.3%) | 1.192 | 0.413 |
10 年後の中央値は、A の場合 1.611, B の場合 1.363 です。リスクが大きくなればなるほど、期待リターン(平均値)と中央値の隔離は大きくなります。
期待リターンは一部の「ラッキー」な人の影響を強く受けてしまうので、期待リターンのみを見るのはやめましょう。それはあまり意味がありません。極端なことをいえば、リスクを増やすことで、分布グラフを右に伸ばすことでいくらでも可能であり、その一方、左側はゼロ以下には伸びません。そのため、リスクを増やすことで期待リターンを 見かけ上 いくらでも増やすことができてしまいます。レバレッジをかければかけるほどリターンが高くなります。
期待リターンよりは、むしろ中央値のほうが「信頼」できます。中央値はリターンとリスクの両方の影響を受けます。中央値は、リターンが大きくなればなるほど大きく、リスクが大きくなればなるほど小さくなります。
資産運用においては、リターンが同じであれば、リスクが小さければ小さいほどよいです。リターンをリスクで割った値、いわゆる「効率」がもっともよいのは、さきほど述べたように、理論上、時価総額加重平均インデックスです。「時価総額加重平均に基づくインデックスファンドだけ買っておけばよい」というのは、決して手抜きというわけではなく、それが最も投資効率を高めるからです。
どうして投資効率として「リターンをリスクで割る (= return / risk) 値を採用するの? リターンをリスクで引く (= return - risk)、あるいは (return / (risk)^2) とか別の計算式じゃないのはどうして?」と 一部の人は疑問に思うかもしれませんが、リターンをリスクで割るのは、決して適当な式というわけではなく、ちゃんと理論的に意味がある式です。詳しくは省略。
以下は興味のある人向けです。とばして読んでも構いません。
これらのチャートは、株価は幾何ブラウン運動に従い、その変動は対数正規分布になるという標準的なモデルに基づいて描きました。
詳細は省きますが、中央値について要点だけここで述べておきますと、リターンを m
(1.0 ベース)、リスクを s とした場合、以下の μ の値:
$$ \mu = \ln m - \ln ( (s/m)^2 + 1) / 2 $$
が中央値のよさを表すと考えればよいでしょう。この μ は大きれば大きいほどよいです。
例: リターン 5%、リスク 5% の場合:
$$ \mu = \ln 1.05 - \ln ( (0.05/1.05)^2 + 1) / 2 \simeq 0.048 $$
例: リターン 5%、リスク 20% の場合:
$$ \mu = \ln 1.05 - \ln ( (0.20/1.05)^2 + 1) / 2 \simeq 0.031 $$
μがプラスであれば、資産運用の年数がたつにつれて、中央値は増加していきます。μがマイナスであれば、資産運用の年数がたつにつれて、中央値は減少していきます(0 に近づいていきます)。
リターンが プラス (=> m が 1.0 より大きい)であっても、リスクが大きい場合は、μ がマイナスになりえます。これは中央値の観点ではどんどん損する「マイナスサム」のゲームと考えるべきであり、そのようなゲームには決して参加してはいけません。
参考) Lognormal property of stock prices assumed by Black-Scholes (FRM T4-10), Why Lognormal Distribution is Used to Describe Stock Prices
長期投資でリスクはへらない
長期投資ではリスクは減るってききました?本当ですか?
「長期投資をすることでリスクを減らせる!」という説明はよく見かけますが、残念ながらそのような事実はありません。事実は逆で「ブレ幅」は時間とともにどんどん拡大していきます。
「リスク」という言葉は曖昧に使用されることが多いですが、ここではきちんと定量的にあらわすためにリスクとはリターンのブレ・すなわち標準偏差 $ \sigma $ をあらわすものとします。これはこの記事のみならず、一般的にもリスクの定量化の方法として広く用いられているものです。
最初に事実をまとめておきましょう。
- どんなに個人が長く投資していしようと、「商品の各年における一年あたりのリスク」 $ \sigma $ には何の影響もありません。それは個人の投資期間とは一切関係ありません。
- 「商品を n 年間保有するとして、その n 年間における成績のブレ・標準偏差」 を $ \sigma _ n $ とした場合、これは $ \sqrt{n} \sigma $ になります。つまり投資期間が長くなればなるほど、n が大きくなればなるほど、 $ \sigma _ n $は減るのではなく増えていきます。これは前述の図の「1 年目の 成績の分布」と「10 年目の成績の分布」からも明らかでしょう。
つまり「長期投資しても成績が一定の値に収束するわけではなくて、むしろ成績のブレはどんどん広がっていく」が正しいです。
「n 年での リスク $ \sigma _ n $ が $ \sqrt{n} \sigma $ になるということは、それを n で割ると $ \sigma / \sqrt{n} $ になるので、一年あたりのリスクは $ \sigma $ よりも小さくなるのでは!」と思わず考えてしまいがちですが、「n 年でのリスクを n で割るという行為」は統計的には何の意味もない操作です。それで 「一年あたりのリスク」が計算できるわけではなく、「一年あたりのリスク」は $ \sigma $ のままです。「標準偏差を期間で割った結果得られる数字」はもはや「標準偏差」を意味しておらず「統計的には何の意味もない数字」であることに注意してください。
「でも投資期間は長くなるほど、年次リターン のぶれは小さくなると聞きました!」と不思議に思った人もいるかもしれません。例えば、以下のような説明です。
- 1 年間投資したときの幾何平均リターンのブレ: -35.0% から +60.0% までの間に収まる
- 30 年間投資したときの幾何平均リターンのブレ: +2.5% から +10.0% までの間に収まる
こうして見ると一見「幾何平均リターン」は収束しているように見えます。しかし、これに基づき実際の「結果リターン」を計算してみると
1 年後:
- $ 0.65 ^ {1} = 0.65 $
- $ 1.60 ^ {1} = 1.60 $
30 年後:
- $ 1.025 ^ {30} = 2.09 $
- $ 1.10 ^ {30} = 17.45 $
であり、1 年間では最大で 2.5 倍の差だったものが、30 年間では 最大で 8.3 倍の差がつく結果になる、つまり「ブレが広がっている」という先程と同じ事実を示しています。
長期投資をしてもリスクは減らないことは理解できました。でも長期投資すると元本割れリスクは減りますよね?!
「でも長期投資をすると元本割れリスクは減りますよね?!」と不思議に思ったかもしれませんが、これもやはり「リスク」を違う意味で使用していることから起きています。
きっと質問で聞きたかったことは「元本割れ標準偏差(?)」ではなく「元本割れする確率」でしょう。
もとの商品の性質にもよりますが、よい商品であるならば、一般には「長期投資すると元本割れする確率を減らせます」は正しいです。
先程の図、リターン 5%, リスク 5% の場合を、見てみましょう。年数とともに 成績が 1.0 を下回る確率は減ることがわかります。

一方、リターン 5%, リスク 20% の場合は、そうとはなっていないことがわかります。10 年たっても、1.0 を下回る確率は高いままであることがわかります。

つまり「長期投資をして元本割れする確率は減らしたい」のであれば
「現金 100%にしましょう。元本割れする確率は 0%です」
...というのは冗談のようで本当ですが、実際はリターンも得るのが資産運用の目的ですので「良質な商品つまりもっともシャープレシオの高い商品であるインデックスファンドと現金でアセットアロケーションを組みましょう。」が「長期投資をして元本割れする確率を減らす方法」の正解となります。
為替リスク
インデックスファンドは内部では海外の株式に投資していますが、為替リスクはどうなんでしょうか?
例えば
- S&P500 インデックスのリスクが仮に 20% (実際はこんなに高くありません)
- ドル円の為替リスクが 10%
とします。
さて、S&P500 インデックスとドル円の変動の間に相関がないとした場合、日本円で S&P500 のような(内部では)ドル建ての商品に投資する場合、日本円で考えた場合のトータルのリスクはどのようになるでしょうか?
この場合はトータルのリスクは 10% + 20% = 30% と単純に足した値になるのではなく、22.4% になります。
$$ \sigma ^ 2 = 0.2 ^ 2 + 0.1 ^ 2 + 2 * 0 * 0.2 * 0.1 = 0.05 $$
$$ \sigma = \sqrt {0.05} = 0.224 (22.4 \% ) $$
つまり為替リスクが 10%だからといって、そのまま 10% リスクが増えるわけではなく増加分は 2.4 % です。そのため(内部で)ドル建ての商品に投資するときに、必要以上に為替リスクを恐れる必要はありません。
北斗神拳
さきほどは最大損失額を 50%としていましたが、インデックスファンドの価格がゼロになることはないのでしょうか?とても心配です。
インデックスファンドの価格がゼロになるとすれば、それは資本主義が崩壊、貨幣経済もおそらく崩壊、現金もおそらく意味がなくなっている世界です。いわゆる、北斗の拳のような ヒャッハー な世界、物々交換な世界になっているでしょう。
そのような事態を心配するのであれば、むしろ北斗神拳を今のうちから身に着けてそのような事態に備えておくべきです。
Q&A編
トービンの分離定理
私はインデックスよりも大きなリターンがほしいからインデックスに加えて個別株にも手を出しています。いけないでしょうか?
投資効率の観点では、個別株は分散が大きくなる(= リスクが大きくなる)要因であり、投資効率が下がります。資産運用が趣味ではない普通の人が、時間をつかってまで個別株に手を出す必要性はありません。
「言葉で説明されてもわかりません!」という方、では、先程の例で使用した
- A (risk: 5%)
- B (risk: 20%)
A と B それぞれについて、10 年後ではなく 40 年後の成績の分布を比較してみましょう。
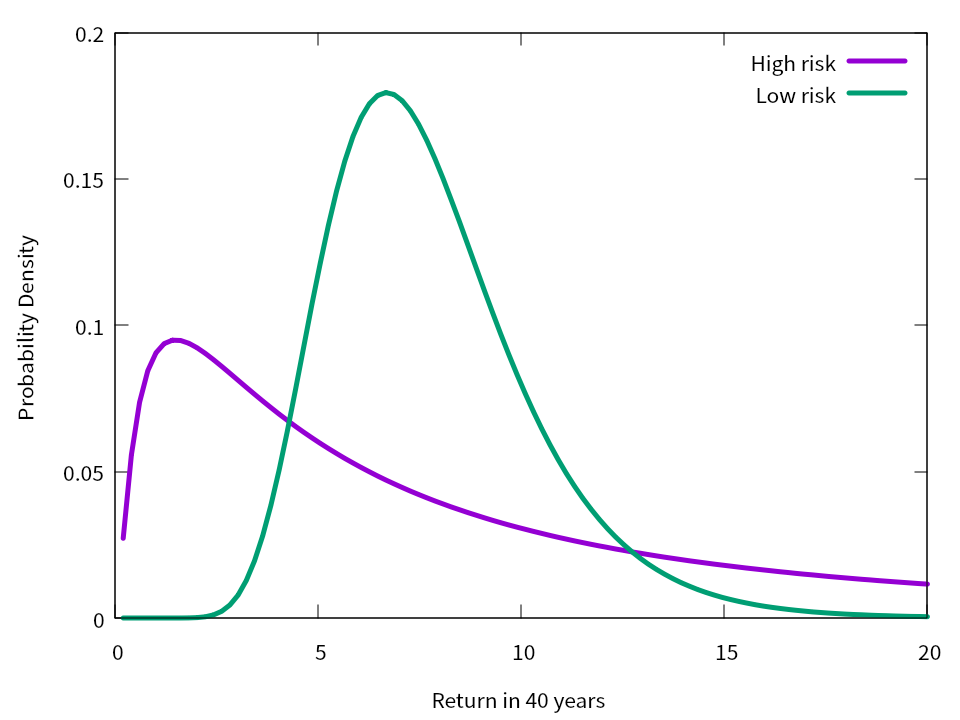
これはやや極端な例ですが、これを見てどちらが「個別株」でどちらが「インデックス」に相当するのかわかりますか?
「個別株はリターンが大きいはず!分布のピークが右側にある・リターンが大きい方が個別株でしょ!」
と思った方、残念ながら間違いです。脳内にあるであろう個別株のイメージを早急に修正する必要があります。実際はその逆です。分布のピークが右側にあるほうが「インデックス」に相当します。
インデックスが最適化するのは、シャープレシオ(= リターン/リスク)です。リターンでもリスクでもありません。
個別株が含まれるアセットアロケーションから個別株を除いて、その分インデックスの割合をより多くすることによって、元のアセットアロケーションよりも一方的に有利なアセットアロケーションをつくることが可能です。
結論編で述べたアセットアロケーションでは、「現金」と「シャープレシオが最適の商品」の2つだけを組み合わせて、アセットアロケーションを構成しています。その一番の理由は「これが楽だから」ではなく「この 2 つだけでどのようなリスク許容度であろうと、同じリスクのなかでもっともリターンが高いアセットアロケーション」を構成できるからです。別の言い方をすると同じリターンでもっともリスクが低いとも言えます。
この定理には名前がついています。トービンの分離定理といいます。
「赤 (Red)、緑 (Green)、青 (Blue)」が「光の三原色」であり、この3色を混ざることによってどんな色もつくりだせるのと同じように、「現金」と「インデックスファンド」は「アセットアロケーションの二原色」です。この2つを混ぜることによって、どんなアセットアロケーションをもつくることが可能です。そしてこの2色から成り立つアセットアロケーションは、ほかの「色」を混ぜてしまったアセットアロケーションよりも「同じリスクでリターンが高く」なります。
例
以下のような2つの商品 A (インデックス)、B (ある個別株) があったとします。
- A (インデックス) は最もシャープレシオがよい商品と仮定します。
- B (個別株) は A よりもハイリスク・ハイリターンですが、シャープレシオは A に劣ります (A: 0.5 > B: 0.45)。
| リターン | リスク | シャープレシオ (= リターン/リスク) | |
|---|---|---|---|
| 商品 A (インデックス) | 5% | 10% | 0.5 |
| 商品 B (個別株) | 10% | 22% | 0.45 |
このとき、ある個人投資家が:
「私は現金とリスク資産の比率は 50:50 にしています。ただし、A (インデックス) のリターン 5% では物足りないので、リスク資産として A (インデックス) だけでなく、リターンが 10% である B (個別株) もいれたいと思います。 A、B は同じ割合(= 全体の 25%ずつ)にすればバランスがとれているでしょう」 と考えたとしましょう。
このアセットアロケーション 「現金:A:B = 50:25:25」 の資産全体のリターン・リスク・シャープレシオはそれぞれ:
- 資産全体のリターン:
3.75%(= 0.05 * 0.25 + 0.1 * 0.25) - 資産全体のリスク:
8.0%(= 0.10 * 0.25 + 0.22 * 0.25) [*1] - 資産全体のシャープレシオ:
0.47(= 3.75 / 8.0)
になります。
B (個別株)を全く使用することなく、A (インデックス) だけを用いて、これよりも有利なアセットアロケーションを作成することが可能です。例えば、以下のようになります。
アセットアロケーション「現金:インデックス = 20 : 80 」
- 資産全体のリターン:
4.0%(= 0.05 * 0.8) - 資産全体のリスク:
8.0%(= 0.1 * 0.8) - 資産全体のシャープレシオ:
0.5(= 4.0 / 8.0)
前者と後者のアセットアロケーションを比較すると次のようになります。
| 現金の割合 | A (インデックス)の割合 | B (個別株) の割合 | 資産全体のリターン | 資産全体のリスク | 資産全体のシャープレシオ | |
|---|---|---|---|---|---|---|
| アセットアロケーション 1 | 50% | 25% | 25% | 3.75% | 8.0% | 0.47 |
| アセットアロケーション 2 | 20% | 80% | 0% | 4.0% | 8.0% | 0.5 |
後者(アセットアロケーション 2) は前者(アセットアロケーション 1) をアウトパフォームします。
- アセットアロケーション 2 はアセットアロケーション 1 と同じリスク (=
8.0%) [*2] にもかかわらず、高いリターン (= 4.0% > 3.75%) が期待できます。 - 逆にいいますと、アセットアロケーション 1 は アセットアロケーション 2 と同じリスクをとっているにもかかわらず、そのリスクに対する見返り(リターン)が少ないです。つまり「リターンを生み出さない無駄なリスクをとっている」です。
まとめますと:
- リターンとリスクは常に資産全体で考えましょう。
- 「資産全体で高いリターンを求めている」のであれば、ハイリスク・ハイリターンの個別株等(ただしシャープレシオはインデックスに劣る)をポートフォリオにいれるのではなく、まずは先程のアセットアロケーション 2 のように(シャープレシオが最適な)リスク資産の割合を増やすのが正しいです。そのほうが、資産全体としての投資効率がよくなる・リターンが大きくなります。
- A 以外のものをポートフォリオに入れる必要があるとすれば、それは「A にフルインベストメント (= 現金:A =
0:100)」よりもハイリスク・ハイリターンを求めるときのみです。ただし、そこまでリスク許容度が高い人は稀でしょう。つまり、A 以外のものをポートフォリオに入れる必要ははありません。
元の質問「私はインデックスよりも大きなリターンがほしいからインデックスに加えて個別株にも手を出しています。いけないでしょうか?」に対する答えを繰り返しますと
- 大きなリターンがほしいなら、インデックスオンリーにしましょう。
- リターンが欲しくない、リターンを小さくしたいのであれば、個別株を混ぜましょう。
が答えになります。質問者はこのような答えはまったく予想していなかったでしょう。なぜそのようなギャップが生じるかというと、リターンを違う意味で使用しているからです。この記事ではリターンは 将来の期待される成績の中央値 (上位 50%の成績) のことを指していることが多いですが、質問者はリターンを「宝くじのリターンは 3 億円です!」と同じ意味で、すわなち「もっともうまくいったときのリターン」(上位 1%等) という意味で使用している可能性が高いです。
「もっともうまくいったときのリターン」の大きさを追求するのであれば資産運用などしないで「宝くじにフルインベストメント」しましょう!
もちろん宝くじの正しい意味での「リターン」は実際にはマイナスです。
- [*1] ここでは、AB の相関は無視しています。
- [*2] 「リスクが同じといっても、リスク資産がすべてなくなったときのダメージは、アセットアロケーション 2 のほうが大きいですよ!」と思わず考えてしまいますが、それは「リスク資産が瞬間的に減少する」というありえない前提にもとづいています。通常はアセットアロケーションのバランスを保つために定期的にリバランスをしますので、同じリスクを取り続けている限り、仮に資産が減るとしても、資産の減り方はどちらもほぼ同じです。
私は若いときは個別株でリスクをとっていきたいです!将来、ある程度、資産形成ができたらインデックスにしたいと思います!
トービンの分離定理に従うと、それは間違いです。
「若いときにリスクをとり、将来、ある程度、資産形成ができたらリスクを減らした資産運用をしたい」のであれば、例えば
- 若いとき:「現金 20%: インデックスファンド 80% 」
- 将来: 「現金 70%: インデックスファンド 30% 」
にするのが正しいです。
「リスクを調整」するために「リスク資産の種類を変える」ことを推奨している記事はこの世の中には多くありますが、それらはすべてトービンの分離定理に反している、つまり「投資効率」を落とす結果になります。
「リスクを調整」するのはあくまで「無リスク資産」と「リスク資産」の保有割合を変えることで調整するのが正しいです。「現金」というのは「最強の無リスク資産」であり、資産運用において何事にも代えがたい重要な役割を果たします。
オルカンとS&P500
インデックスファンドとしては、アメリカ株 (S&P500 や VTI)100%でよいのでしょうか? それとも、オルカン のように全世界株のほうがよいのでしょうか?
どちらを選ぼうと、大きなミスにはならないでしょう。このあたりまでくると、どちらも正解です。 99 点 vs 98 点とかそれくらいの差だと思います。
理論上、もっとも投資効率がよくなるのは時価総額荷重にもとづいて保有することですが、その母体となる「世界 (ユニバース)」は広ければ広いほどよいです。 この観点においては、全世界のほうが「世界」が広いため、全世界株式のほうがよいです。
- 世界の広さ: 全世界 > S&P500
ただし、現実では、保有に必要なコストを考慮する必要があります。コストというのは、表面上知ることができる信託報酬だけの話だけではありません。実際は目に見えない様々なコストが間接的にかかっており、その観点では S&P500 のほうがコストが低い・つまり優秀といえます。
- コストの優秀さ: S&P500 > 全世界
つまり、一長一短であり、どちらがよいかはそれぞれの程度しだい、定量問題です。
「世界の広さ」の観点では、S&P500 ほどの広い世界であればほぼ十分効率的といえます。全世界と比較して大きな差が生まれるほどではないでしょう。
「コスト」の観点では、全世界の株式を保有するためのコストは、金融技術が発達・投資環境が年々整備されるにつれ下がっており、S&P500 と比較してそれほど引けをとっているわけではありません。
つまり、どちらであろうともはや大きな差はないでしょう。迷うくらいなら、普通にオルカン等の全世界株でよいと思います。
ここまでの話において「S&P500 の過去のリターン」あるいは「アメリカが今後も成長するかどうか」等は保有するべき理由として一切言及していません。それらを理由とするのは間違っています。
つまり
- 「S&P500 のほうが過去のリターンはよかった!私はこれからもアメリカが伸びると予想しています!だから S&P500 です!」
は保有する理由としては不適切です。あくまで、基本は、
「なるべく広い世界を対象にして、余計なことを考えずに、時価総額荷重で株式を保有する。ただし現実的にはコストがかかるためコストを考慮して商品を選択する」
です。その結果、たまたま S&P500 の商品が選択肢として選ばれるのは、OK ですが、その商品の過去リターンがよいのは「ただの偶然」と考えましょう。決して「過去リターン」を理由に選んではいけません。
それでも私はどちらにするか選べません!選べないから私はどっちも半分ずつもちます!それってだめですか?
「選べないから私は全世界株と S&P500 を半分ずつ!」という方もいらっしゃると思いますが、おそらくそれらは
「なんとなく全世界のほうが安全そうだけど、S&P500 の過去リターンを見ていたら、そっちも捨てがたい!悩む!」
という「ゆるふわ」な考えからでしょう。そのような特定の商品・インデックスの特定の期間の「過去リターン」を理由に商品を選択するのは、典型的な「余計なこと」です。
なお「半分ずつもつ」というのは実際にはそこまで投資効率を落とすというわけではありません。それぞれの商品が 99 点 vs 98 点だとしたら、半分ずつもつのは 97 点くらいといってよいでしょう。
「半分ずつもった」からといって「結果のリターン」がちょうど両者の成績の中間になるとは限りません。実際には「どちらにも負ける」ことが起こりえます。結果が「単純に足して 2 で割った成績」、いわゆる算術平均にならないのは、 50% + 50% のバランスを保つために定期的にリバランス等を行うからです。もしリバランスを行わないのであれば、それはもはやポートフォリオとは呼べるものではなく、もはやこの議論の対象外です。:)
気をつけたいのは、そのような余計なことをする人は、おそらく将来も「その時点での過去リターン」にもとづいて余計なことをする可能性があるということです。 将来「直近 5 年のリターンは XXX 国ファンドがいい!これもちょっと買っておく!」等、やってしまうでしょう。それらを繰り返すうちに、結果、時価総額荷重からはますます遠く離れて、投資効率を大きく落とすことになるでしょう。
「私はそのような余計なことを将来してしまいそう...」と不安な方は、最初から全世界株のみでよいと思います。悩む必要はなくなりますし、悩んでも何も得るものはありません。
債券
リスク資産として株式だけでなく債券も入れたほうがよいといわれたのですが?
「普通の人」はリスク資産は株式 100%でいいと思います。
「株式と債券」などのようにリスク資産を 2 種類以上持ち、それを組み合わせたアセットアロケーションをつくるのは、普通の人にとっては難しすぎると思います。普通の人がそれをしたからといって、結果として得られるリスク資産の全体の投資効率(シャープレシオ)が、もともとのリスク資産 1 種類(市場ポートフォリオ)の投資効率を上回ることはまずありません。
株式と債券の割合をどうすれば、理論上、シャープレシオが株式の市場ポートフォリオを上回るのか、現実問題として不明瞭です。現在、出回っている株式と債券を組み合わせた商品はこのあたりの割合が理論的根拠に乏しいもののが多いです。特に何の根拠もなく半分ずつとしている、あるいは過去の実績から株式と債券の割合を決めている商品等です。このあたりの問題は現実的には未解決・金融技術が追いついていないと言えるでしょう。
それよりは、リスク資産はシンプルに 1 種類だけにしておき、アセットアロケーションをシンプルに保ったほうがよいでしょう。簡単にリスクとリターンを把握できるし、リスク・リターンの調整も簡単です。リスクとリターンの調整は、あくまで、現金とリスク資産の割合で行いましょう。
「債券をいれたほうが変動がマイルドになる」と同じ効果を得たいなら、単にリスク資産の割合を減らすだけでよいです。
これは債券に限った話ではありません。「銘柄の組み合わせが...」「最適なポートフォリオーを組むには株式と債券と金を...」といった資産運用に関する記事は未だに多く見かけますが、個人で複数のリスク資産を組み合わせてポートフォリオを工夫して組む必要性はありません。
いまは、全世界株等の投資信託(市場ポートフォリオ)の商品を 1 点だけかっておけば、リスク資産に関しては自然とほぼ最適なシャープレシオのポートフォリオになります。もともとそのためのインデックス投資であり投資信託です。個人でがんばってポートフォリオ組む必要性があったのは昔の話です。
海外ETF
投資信託をオススメしているようですが、海外 ETF を直接購入するのはどうでしょうか?
TODO: 海外 ETF を買う必要性はもはやないに等しい、買う人もほとんどいないでしょうから、このセクションは削除予定。
手間は気にしない、外国税額控除をきちんとするのであれば、ETF が依然としてコストの観点では若干有利です。ですが、ほとんど差がない、99 点が 99.1 点になるといった誤差レベルですので、あえて手間をかけてまで ETF を直接購入する必要はほとんどの人にとってはないでしょう。特に 新 NISA では外国税額控除が利用できないので、分配金をださない投資信託でよいです。
参考) 計算結果 (in Rust)
マーケットタイミングを読まない
「今は高値だから現金を貯めておいて暴落時に買おう」はどうしてだめなのでしょうか?一見うまくいきそうなのですが。
「今は株価は高値だから買うのは控えて現金をためておこう。暴落したら買おう」と思ってしまうのは人間としての自然な心理ですが、それは机上の空論です。それが継続的にうまくいくことは決してありません。
以下にそれを証明します。
例えばインデックスファンド 楽天 VTI を買っている人がいるとしましょう。
その人が「今は 楽天 VTI の株価は高値だから買うのは控えて現金をためておこう。暴落するときを待ってそのタイミングで買おう」という戦略をたてるとします。
もしその戦略が「うまくいく」と仮定します。すると、なにが起きるでしょうか?
そのような戦略がうまくいくなら、いまごろ「そういうことをする」ファンドが登場しているはずです。
たとえば、SBI 証券から
「SBI 「楽天 VTI」 を暴落時に買うファンド」
が登場しているはずです。このファンドの運用方針は:
- 「楽天 VTI」 の価格が高いときには「楽天 VTI」 を購入するのではなく現金としてためておく
- 「楽天 VTI」 の価格が暴落したときに「楽天 VTI」 を購入する
となります。このファンド「SBI 「楽天 VTI」 を暴落時に買うファンド」の運用成績は「楽天 VTI」の運用成績を上回ります。
すると、今度は楽天証券から
「楽天 「SBI 「楽天 VTI」 を暴落時に買うファンド」を暴落時に買うファンド」
が登場することでしょう。このファンドの運用方針は:
- 「SBI 「楽天 VTI」 を暴落時に買うファンド」 の価格が高いときには「SBI 「楽天 VTI」を暴落時に買うファンド」を購入するのではなく現金としてためておく
- 「SBI 「楽天 VTI」 を暴落時に買うファンド」 の価格が暴落したときに「SBI 「楽天 VTI」を暴落時に買うファンド」 を購入する
となります。このファンド「楽天 「SBI 「楽天 VTI」 を暴落時に買うファンド」を暴落時に買うファンド」の運用成績は「SBI 「楽天 VTI」を暴落時に買うファンド」の運用成績を上回ります。
すると、今度は SBI 証券から
「SBI 「楽天 「SBI 「楽天 VTI」 を暴落時に買うファンド」を暴落時に買うファンド」を暴落時に買うファンド」
が登場することでしょう。
このファンド「SBI 「楽天 「SBI 「楽天 VTI」 を暴落時に買うファンド」を暴落時に買うファンド」を暴落時に買うファンド」」の運用成績は「楽天「SBI 「楽天 VTI」 を暴落時に買うファンド」を暴落時に買うファンド」の運用成績を上回ります。
そして、それをさらに暴落時に買うようなファンドが登場するでしょう。
そして、それをさらに暴落時に買うようなファンドが登場するでしょう。
....
このあたりでこのような戦略が机上の空論であるということに気づくと思います。
証明終わり。
(半分、冗談ですけど、それなりに核心はついています。)
もう少し真面目に話をすると、そのような「今は高値だから」という情報はとっくに市場に織り込み済みです。もし、それが本当ならば、プロ中のプロたちは売却をはるか昔に終わらせています。それらの材料を考慮して適正な値に下がった結果が今の価格です。
ドルコスト平均法
さきほどの A さんの例だと、50%を一括で投資していましたが、それでよいのでしょうか?少しずつ分割して投資したほうがよいのではないでしょうか?
あなたは「ドルコスト平均法の呪い」にかかっています。優先すべきは、あくまでアセットアロケーションであり、決してアセットアロケーションを考慮しないで「ドルコスト平均法」自体を「目的」にしてはいけません。
たとえば、50%を:
- 10%ずつ 5 年にわけて分割で投資する (ドルコスト平均法; DCA: Dollar Cost Averaging)
- あるいは、50%を一括投資する (LSI: lump-sum investing)
それぞれの場合、どのようなアセットアロケーションになるか見てみましょう。
(ここでは、簡単化するため毎月のつみたて額は考慮しないとします)
| ドルコスト平均法 | 適切な一括投資 | |
|---|---|---|
| 1 年目 | 90:10 | 50:50 |
| 2 年目 | 80:20 | 50:50 |
| 3 年目 | 70:30 | 50:50 |
| 4 年目 | 60:40 | 50:50 |
| 5 年目 | 50:50 | 50:50 |
| 6 年目 | 50:50 | 50:50 |
| 7 年目 | 50:50 | 50:50 |
| 8 年目 | 50:50 | 50:50 |
| ... | ... | ... |
「ドルコスト平均法」は、A さんのリスク許容度が 50:50 にも関わらず、最初の 5 年間は、A さんはリスク許容度よりも圧倒的に低いリスクしかとっていません。 必要以上にローリスク・ローリターンなアセットアロケーションをとるには、合理的な理由が必要です。
このような「ドルコスト平均法」をとる人の心理は、大抵の場合、「一括投資した直後に暴落がきたらどうするんですか!」だと思いますので、試しに、今後 10 年の間に 1 年だけ暴落(-20%)が起きる、それ以外の年はリターンが 4%という場合、50%部分のそれぞれの 10 年後の成績はどうなるか見てみましょう。
| 暴落が起きる年 | ドルコスト平均法 | 適切な一括投資 |
|---|---|---|
| 1 年目 | 1.302 | 1.139 |
| 2 年目 | 1.237 | 1.139 |
| 3 年目 | 1.174 | 1.139 |
| 4 年目 | 1.113 | 1.139 |
| 5 年目 | 1.054 | 1.139 |
| 6 年目 | 1.054 | 1.139 |
| 7 年目 | 1.054 | 1.139 |
| 8 年目 | 1.054 | 1.139 |
| 9 年目 | 1.054 | 1.139 |
| 10 年目 | 1.054 | 1.139 |
- ドルコスト平均法の場合は、暴落が起きる年によって、最終的なパフォーマンスが変化します。
- 適切な一括投資の場合は、暴落がいつ起きても、パフォーマンスは同じ (= 1.139) です。
つまり、ドルコスト平均法は適切な一括投資に比較して:
- 1 年目に暴落が起きると相当得 (+0.164)
- 2 年目に暴落が起きると得 (+0.098)
- 3 年目に暴落が起きると少し得 (+0.035)
- 4 年目に暴落が起きると少し損 (-0.026)
- 5 年目に暴落が起きると損 (-0.084)
- 6 年目に暴落が起きると損 (-0.084)
- 7 年目に暴落が起きると損 (-0.084)
- 8 年目に暴落が起きると損 (-0.084)
- 9 年目に暴落が起きると損 (-0.084)
- 10 年目に暴落が起きると損 (-0.084)
- ...
となるような(一般にはマイナスサム)な賭けに参加するようなものです。このように「特定の期間に暴落が起きる」ことに合理的な理由もなく賭けることは避けるべきです。すべての情報は株価に織り込み済みと考えるのであれば、このような賭けに参加するべきなのは、自分だけがまだ市場に織り込まれていない特別な情報をなぜか知っているという特殊な状況のみでしょう。 (これはかなり乱暴な議論なのですが、呪いを解くにはしょうがない...)
難しくなってきたので、ここで話を簡単にしましょう。資産運用のリターンは結局のところ「できるだけ多くの資産」を「できるだけ長い年数」市場においておくことでほぼ決定されます。そのため、リスク許容度の範囲内で、「リスク資産の額」x「年数」であらわされる「掛け算の結果」をできるだけ多くするのが重要と考えるとよいでしょう。
例)
適切な一括投資をすることで:
- 「500 万円」x「5 年間」
の資産運用をできる機会があったとしましょう。この際に、適切な一括投資ではなく、たとえば 5 年間に渡って分割投資・ドルコスト平均法を選択するということは、「500 万円」x「5 年間」の資産運用ができる機会があったにもかかわらずその機会を自ら捨てて:
- 「(平均して)250 万円」x「5 年間」
- (別の見方をすれば)「500 万円」 x 「(平均して)2.5 年間」
という選択を自らしているようなものです。「長期投資」が重要だと理解していながら、ドルコスト平均法は自ら「長期投資」する機会を捨てているのです。
ちなみにアセットアロケーションを無視すれば「一括投資 vs ドルコスト平均法」は極論すれば、 期間内において、その部分のみに注目した場合:
- 「現金:リスク資産 = 0:100」(ハイリスク・ハイリターン)
- 「現金:リスク資産 = 50:50」(ローリスク・ローリターン) (期間内の平均。期間後には 0:100 になっていることに注意)
のアセットアロケーションのどちらがよいでしょうか?という話と同じです。どちらもシャープレシオは同じであり、どちらが適しているかは本人のリスク許容度に依存します。
アセットアロケーション全体のリスク許容度を無視して、「一括投資 vs ドルコスト平均法」の優劣を部分的に論じるのは無意味です。
「一括投資」でなくアセットアロケーション全体のリスク許容度を考慮した「適切な一括投資」が重要です。
例: 現状維持バイアスによる「ドルコスト平均法の呪い」
A さんは、長年資産運用を続けてきました。現在の資産は、現金:リスク資産 = 500 万円 :500 万円 です。
さて、ここで次の 2 通りのケースを考えてみましょう。
- A さんは相続(あるいは贈与等)で 1000 万円の 現金 を手にいれました。
- A さんは相続(あるいは贈与等)で 1000 万円分の 株 を手にいれました。
A さんのリスク許容度はいぜんとして、現金:リスク資産 = 50:50 です。それぞれのケースにおいて、 A さんはどのようなアセットアロケーションにするのがよいでしょうか?
この 2 通りのケースに対して、もしあなたが:
「1000 万円の 現金 を手にいれました」 の場合:
「1000 万円の半分の 500 万円を投資に回したい。ただし、一括投資した直後に暴落する「リスク」を避けるため、500 万円は 5 年にわけて分割投資しよう」と考えるのであれば、
アセットアロケーションは次のようになるでしょう。
| 現金:リスク資産 | |
|---|---|
| 贈与前 | 500:500 |
| 贈与直後 (+ 現金 1000) | 1500:500 |
| 1 年目 | 1400:600 |
| 2 年目 | 1300:700 |
| 3 年目 | 1200:800 |
| 4 年目 | 1100:900 |
| 5 年目 | 1000:1000 |
「1000 万円分の 株 を手にいれました」 の場合:
「リスク資産が多すぎるので、贈与された 1000 万円分の株のうち 50%は売却しよう。ただし 500 万円分を一括で売却した直後に株価が暴騰したらもったいない。その「リスク」を避けるため、は 5 年にわけて分割して売却しよう」と考えるのであれば、アセットアロケーションは次のようになるでしょう。
| 現金:リスク資産 | |
|---|---|
| 贈与前 | 500:500 |
| 贈与直後 (+ 株 1000) | 500:1500 |
| 1 年目 | 600:1400 |
| 2 年目 | 700:1300 |
| 3 年目 | 800:1200 |
| 4 年目 | 900:1100 |
| 5 年目 | 1000:1000 |
さて、この辺りで、自分の矛盾に気づいたと思います。前者と後者で 5 年間アセットアロケーションが異なっています。本来、違うアセットアロケーションを選択する必要性はどこにもありません。どちらの場合も、総資産額は 2000 万円であり、リスク許容度は同じです。いずれの場合でもアセットアロケーションは同じであるべきです。
もし、あなたが、このような 2 通りの場合に、違うアセットアロケーションを選択してしまっているのであれば、それは、おそらく現状維持バイアス・ドルコスト平均法の呪いにとらわれているということです。現状(今回の場合は贈与直後の現金:リスク資産の比率)にとらわれすぎると、正しいアセットアロケーションをとる妨げになるということですね。
正しい方針としては、 どちらの場合も
| 現金:リスク資産 | |
|---|---|
| 1 年目 | 1000:1000 |
にすぐにすることです。すわなち、1000 万円分の現金を贈与されたときは 500 万円をすぐに一括投資、1000 万円分の株を贈与されたときは 500 万円を一括売却するのが合理的です。
ドルコスト平均法はだめなんでしょうか?私は給料の中から毎月 3 万円つみたてしているのですが!
大丈夫です。それはおそらくですが「ドルコスト平均法」ではありません。ドルコスト平均法は「つみたて」(continuous, automatic investment)とは違います。
「つみたて」でしたら、なんの問題もありません。それはある意味、1 年に 12 回、「一括投資」しているものです。
ドルコスト平均法はもともと、投資を始めた直後や、相続や贈与などで一時的にまとまった資金を手にいれたときに、(リスク許容度の範囲内で)一括で投資できるにもかかわらず、あえて市場に投入するタイミングを遅らせて分割しながら一定額ずつ入れることをいいます。つまり「ドルコスト平均法」とは「あえてタイミングを遅らせている」つまり「マーケットタイミングを読もうとしている」投資方法です。
実際のところ、ドルコスト平均法自体には(心理面を除いて)魔法のような特別なメリットがあるわけではなく、アセットアロケーションを歪める要因になるだけです。未来を予測する能力がない・マーケットタイミングを決してはかったりはしない「普通の人」にとっては、とても合理的とは呼べる戦略ではありません。
「普通の人」がするのは、「つみたて」と「適切な割合を一括で投資」であって、ドルコスト平均法ではありません。自分にあったアセットアロケーションを維持することがあくまで優先するべきことであって、その手段として「つみたて」と「適切な割合を一括で投資」があります。と考えればよいでしょう。
参考) Dollar cost averaging, Dollar-cost averaging just means taking risk later
でもドルコスト平均法なら「株価が安いときに多く」株数を購入することができます。これってよいことでは?
ドルコスト平均法の説明として、あたかも「株価が安いときは多く買える」ことが「よいこと」であるかのような説明をしている記事は多いです。残念なことに証券会社のサイトの説明にも未だに「ドルコスト平均法」が商品の販促のための材料に使用され、そのようなことがあたかもメリットであるかのように伝えています。
たしかに、例えば、現金 1 万円で株式を 1 万円分購入するとしたら、
- A) 株価が 500 円のときは 20 枚
- B) 株価が 1,000 円のときは 10 枚
購入することになります。これで「A のほうがよい」と考える方、どうか冷静になってください。 A も B もどちらも同じ 1 万円分の価値です。
たしかに、A のほうが枚数は多いですが、枚数が多く買える理由は「一枚あたりの価値が小さい」からです。
わかりやすく例えると 1 万円札を両替するときに
- A) 500 円玉 20 枚に両替
- B) 1000 円札 10 枚に両替
に両替するとして「A のほうが枚数を多く買えた!」と喜んでいるようなものです。
現金 1 万円で購入できる株式はいつだって、その売買の瞬間は合計 1 万円分の価値であり「株数だけ」に注目するのは何の意味もありません。
「でも株数を多く買ったほうがその後株価が値上がりしたときに多く利益がでるのでは?!」
と思った方、冷静になってください。たとえばその後 10% 株価が値上がりしたとしましょう。その際、
- A) 500 * 1.1 * 20 = 11,000
- B) 1,000 * 1.1 * 10 = 11,000
でどちらも 11,000 円です。
出口戦略
出口戦略 / いつ売却すればよいのでしょうか?ここまでの説明だと買うことばかりで、いったいいつ売却(利益確定)すればよいのかわかりません。
ここまでの説明で「いつ売却すればよいのか?」の説明も実はすんでいます。 :)
定期的に(年に 1 回、あるいは数年に 1 回)、アセットアロケーションについて見直 しましょう。
を思い出しましょう。
例えば、65 歳まで 現金:リスク資産 = 50:50 の割合で資産運用をしてきた人がいるとしましょう。
| 現金 | リスク資産 |
|---|---|
| 1,500 万円 | 1,500 万円 |
とします。もう収入はありませんので、年金と現金を使って生活することになるでしょう。
さて、3 年後にはこうなりました。現金は 200 万円減りますが、資産運用は続けていますので、リスク資産は 1700 万円に増加しています。
| 現金 | リスク資産 |
|---|---|
| 1300 万円 | 1,700 万円 |
どうやら、バランスがいつの間にか悪くなっているようです。アセットアロケーションを 50:50 に戻すために、リスク資産を 200 万円分売却することにします。
| 現金 | リスク資産 |
|---|---|
| 1500 万円 | 1,500 万円 |
これで 50:50 になりました。
まとめますと:
- 利益確定のために売却する必要はありません。「利益確定」という概念は捨てましょう。資産運用は一生続くものだと考えましょう。
- 売却する必要があるのは、アセットアロケーションのバランスを保つときだけだと考えましょう。
定期売却サービス
さきほどのようなパターンが続くのであれば、この作業を自動化してくれるサービスもあるようです。
ロボアドバイザー
ロボアドバイザーってどうなんでしょうか?
記事の公開にあたってこの部分は削除しました。
レバレッジ
レバレッジ型商品はどうでしょうか?!
レバレッジというといかにも怪しそうですが、レバレッジはリスク・リターンを調整するためのきちんとした手法のひとつです。ただし、「普通の人」があえて高いリスクをとってまで高いリターンを求める必要が本当にあるかは、慎重に判断する必要があるといえます。
すくなくともレバレッジは「高コスト」という明確なリターンへの影響があるので、それらを十分理解した上で、よほどの特殊な状況におかれている一部の人を除いては、必要ないでしょう。
アセットアロケーション的には、レバレッジは、例えば「現金:リスク資産 = -100:200」に相当します。いわゆる「負のアロケーション」を含むアロケーションです。「現金:リスク資産 = 0:100」よりもハイリスク・ハイリターンになります。ただし、コストの分だけ、投資効率は低くなります。
レバレッジのリスクは高いのは理解していますが私は耐える自信があります!「リスク許容度」は高いです!
それは頼もしいですね。「リスク許容度」という言葉は割と誤解を生みやすい言葉であり、「許容」という言葉からつい「耐えることができるかどうか」というメンタルだけの問題だと想像してしまいますが、前述のとおり、リスクは「実際の」リターンに確実に影響を及ぼすものです。残念ながら「耐えれば OK!」では済みません。
理論的な話を少しするならば、レバレッジはかければかけるほどリターンがあがるという性質はもっていません。事実はその逆です。レバレッジ倍率をあげていくと途中からリターンが逆に下がるという現象がおきます。
なぜそのような現象がおきるか詳細はなるべく省いて簡単に説明します。以下は興味のある人向けです。とばして読んでも構いません。興味がなくても最後の図だけでも見ていってください。
時刻 $ t $ における ある商品の価格 $ S_t $が幾何ブラウン運動に従うというモデル:
$$ d S_t = \mu S_t dt + \sigma S_t d B_t $$
において、レバレッジを $ L $ 倍かけたとします。
$$ d S_t = L \mu S_t dt + L \sigma S_t d B_t $$
その結果、時刻 $ t $ における価格の中央値(= 価格の対数期待値と一致します)$ M_t $ は
$$ M_t = S_0 \exp \left( \left(L \mu - \frac{L^2 \sigma^2}{2} \right)t \right) $$
になります。 $ \mu $, $ \sigma $ を定数、$ L $ を変数とし、指数部分に注目すると
$$ L \mu - \frac{L^2 \sigma^2}{2} $$
これはみなさん中学生のときに学習したおなじみの上に凸な二次関数です。レバレッジ倍率 $ L $ とリターンの中央値の関係をプロットすると以下のようになります。 $ \mu $ = 5%, $ \sigma $ = 20% の場合です。
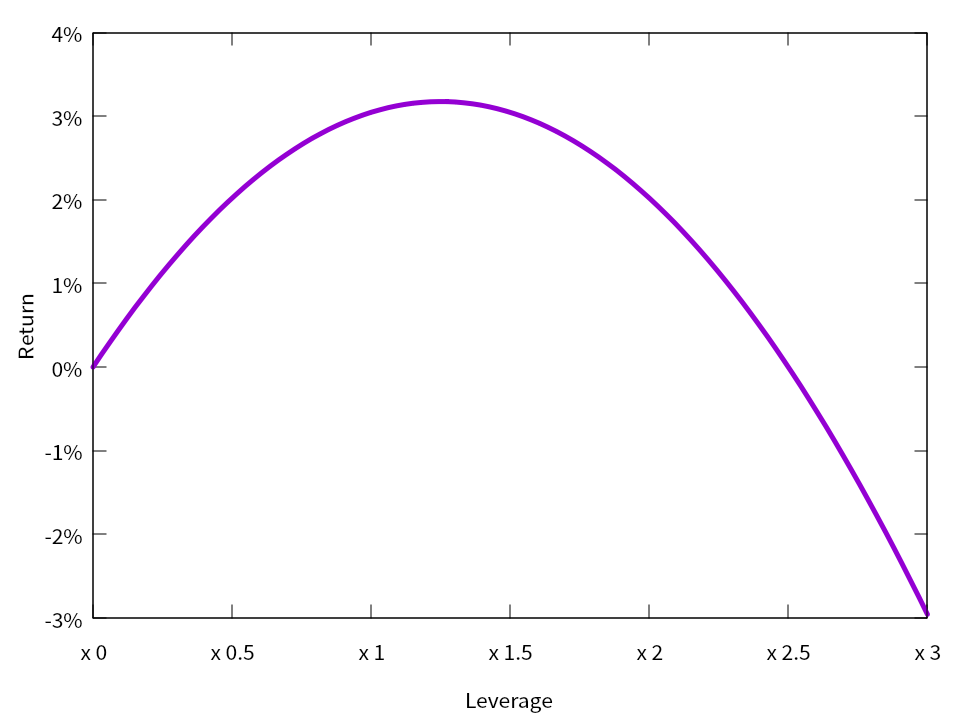
この場合は、レバレッジ倍率 L を大きくするにつれて、リターンの中央値・ 対数期待値はレバレッジ倍率 1 倍、つまり通常の「フルインベストメント」までは「ほぼ」線形にリターンが増えていきます。しかしそれを過ぎるとリターンがあまり増えなくなります。途中からはむしろ逆にリターンが下がっていき、3 倍までいくとリターンはプラスどころかむしろマイナス、つまり資産が減ることになります。
このような性質があるため、たとえば 「FX で 50 倍!」のような極端なレバレッジ倍率は破産する・資産がほぼゼロになる確率が時間とともに 100% になっていきます。
株式におけるレバレッジも同じです。しきい値を超えてレバレッジ倍率をあげればあげるほどリターンが上がるどころか逆に下がってしまいます。レバレッジの高コストを払い、さらにリスクをとっているのに、逆にリターンが下がるといういわゆる「ふんだりけったり」になってしまいます。
世の中には「レバレッジ 50 倍をかけて FX で大儲け!」「資産が少ないなら信用取引をしましょう!信用取引は危ないイメージがありますがどんな手法も使い方次第です!」等の甘い誘惑があります。資産が少ない私はこれらに手を出した方がよいのでしょうか?
絶対に手をださないでください。
高配当
私は定年まではインデックス投資で資産を増やし、定年前後には高配当株に乗り換えて配当金生活を送る予定です。この戦略はどうでしょうか?
やめましょう。典型的な「余計なこと」のひとつであり、投資効率が落ちるだけです。いろいろな面で「相当」落ちます。
先程述べたように、定年後に定期的に現金が必要になるのであれば、証券会社の投資信託定期売却サービスを利用すればよいでしょう。それが「配当」の代わりになると考えるほうが筋がよいでしょう。
「配当」のために、インデックス投資と比較して一般に投資効率が低い・リターンが低いとされている高配当株にあえて定年前後に乗り換える合理的な理由はありません。
なにより定年前後で乗り換えのために一度にリスク資産を売却すると、譲渡益に対する税金をそのタイミングで一度に支払わないといけません。税金を支払うのはできるだけ先送りにしたほうが投資効率はよいです。
そうはいっても配当がもらえるって嬉しいじゃないですか!高配当株はだめなんですか?
それは「給料は銀行振込で 20 万円振り込まれるよりも、現金で 19 万 9000 円直接手渡しされるほうが嬉しいです!」という発想とたいして変わらないと思います。
高配当投資・配当をだすことが資産運用の効率をいかに下げるか、その非効率さが長期投資になればなるほどどれほど顕著になるか、単純な設定で計算してみましょう。
商品がふたつあるとします。フェアに比較するためどちらもトータルリターンが 5%とします。ただし、一方は
- A) リターンの 5%分すべてを配当としてだすいわゆる高配当株
もう一方は
- B) インデックスファンドであり分配金は一切ださない
とします。
なお配当は税金 20%分を除いてすべて再投資するとします。投資するのはどちらも特定口座で行います。
この条件で 100 万円を 60 年間運用するとしましょう。その結果、税引き後の資産額は前者の高配当株の配当再投資の場合は
- A) 1,052 万円
後者の無分配のインデックスファンドの場合は
- B) 1,514 万円
になります。資産額として 50%近い差がうまれます。
よかったら自分で計算してみましょう。これは「税金の支払いを先送りする」ことが資産運用において如何に長期で有利に働くかというよい例です。結論編で述べた iDeCo のお得度が高い理由もここにあります。
なお新 NISA のような非課税口座で運用する場合はこのような差は生まれませんが、それでも高配当投資は配当を再投資する際、新 NISA の枠をその分多く使用することとなり、それは「新 NISA の枠が小さくなる」と同じ効果といえます。
どちらにせよ資産運用にあたって、無分配と比較した場合、配当はなにもよいことはありません。配当再投資とは例えるなら
「銀行口座から手数料を払って ATM でお金を引き出し、そして引き出したお金をすぐに銀行口座に入金している」
行為を繰り返すようなものです。 一見ほんのわずかな差に思えることも、資産運用という「複利の世界」では「断続的に損な行為を繰り返す」ことは長期では大きな差をつけられる要因になります。
その他のよくある質問と答え
すでに特定口座で 500 万円ほど運用しています。含み益が 100 万円ほどあります。新 NISA がはじまる際、特定口座の資産を売却して新 NISA に移したほうがよいでしょうか?
新 NISA に移したほうがお得になるかどうかはさまざまな条件によって異なります。
売却に伴う譲渡益にかかる税金を払ってでも非課税枠に移したほうがほとんどの場合得です。ですが、本人がその年に利用したい政府の制度(分離課税なら問題ないでしょうが、一部の制度は総合課税の所得をチェックします)、あるいは本人の今後の収入・つみたて額等を考えると移さないほうがよいケースもあります。総合的に考えましょう。
一般解を簡潔に述べるのは困難ですので、ここではいくつかの具体的な例をあげるにとどめておきます。ただし先程述べた理由で必ずそうとはいえないケースもあることに注意してください。
A さんの場合
A さんは 2023 年 12 月の時点で特定口座で 500 万円運用しています。2024 年以降、A さんは新 NISA には毎月 10 万円つみたてできます。
- 2024 年: 特定口座から(税引後)240 万円分を新 NISA に移しました。毎月のつみたて 10 万円 分とあわせて、2024 年は 新 NISA の枠の上限 360 万円使いきりました。
- 2025 年: 特定口座から(税引後)240 万円分を新 NISA に移しました。毎月のつみたて 10 万円 分とあわせて、2025 年は 新 NISA の枠の上限 360 万円使いきりました。
- 2026 年: ...以下、同様です。新 NISA の枠が使い切れないのであれば適宜、特定口座から移したほうがよいでしょう。
B さんの場合
B さんは 2023 年 12 月の時点で特定口座で 500 万円運用しています。2024 年以降は、B さんは新 NISA には毎月 30 万円つみたてできます。
この場合は
- 2024 年以降: 毎月のつみたて 30 万円 だけで、新 NISA の枠が上限一杯まで使用できるので、特定口座の資産には手をつける必要はありません。
ここではわかりやすい例を 2 つだけ示しました。それ以外のケースや詳細にはここでは触れません。 自分で実際に計算してどちらがお得になるか計算してみることをおすすめします。
資産運用ってもっと一攫千金の夢があるものだと思っていました!
そんなものはありません。フリーランチは存在しません。いままで平均点以下だったわれわれ「普通の人」が時間をほぼ使うことなく「理想的な点数」をとれるだけで十分ありがたい話です。実際、これより上の方法を目指しても 99 点が 100 点に近づくだけであり、多くの場合は余計なことをして逆に点数を下げてしまうだけです。
市場平均で必要十分であると理解するメリットのひとつとして、世の中にあふれるぼったくり商品に騙されにくくなるということです。
この記事のタイトルにあえて「70 点」などの謙遜した点数ではなく「99 点」とつけたのは、下手に「70 点」とかつけてしまうと「もっと 100 点をとれるようなよい方法があるのではないか?」と思わせてしまうのはよくない、と思ったからでした。SNS 等では、投資詐欺・アフィリエイター・悪質な商材屋等がはびこっており、市場平均が理想的であると理解していない人は、そのような甘い言葉をそのまま受け入れてしまい、「月利 10%!」のようなありえないリターンで誘惑してくるぼったくり商品に騙されしまうでしょう。
夢は資産運用以外で叶えましょう。
インデックスファンドがよいことはわかりました。しかし SNS 等では「インデックス投資は思考停止。勉強にならない。毎日、投資に真剣に向き合うべき」という声があります!
自動洗濯機が登場したとき、洗濯板で洗濯をしていた人たちは
- 「自動洗濯機は思考停止。洗濯は難しいもの。洗濯板での洗濯は毎日が勉強」
と自動洗濯機を利用して楽をする人たちに苦言を呈していたそうですよ。
いつの時代だって自分たちが今まで苦労してきたこだわりがある分野において新しい「技術」が登場したときは、その「技術を利用して楽をする」人たちに苦言を呈してしまいたくなるものです。
- 自動車は思考停止。馬車こそが至高。
- カーナビは甘え。自分で道をすべて覚えるまではドライブに行くな。
- ロボット掃除機は甘え。自分で掃除しないと掃除の技術は身につかない
- キャッシュレスではお金の管理ができない。現金こそが至高。
これらは趣味でやるぶんには何の問題もないでしょう。人の趣味に口をだしてはいけません。ただ洗濯が趣味でもない普通の人が「自動洗濯機」を買おうとしているときに、「自動洗濯機は思考停止」といってくる人が周りにいたら、そのような人たちには近づかないほうがよいでしょう。実際のところ「自動洗濯機」のほうがきれいに洗濯してくれるのですから。
最後に
この記事を書いたのはソフトウェア・エンジニアです。資産運用に関する記事を書くのは今回が最初で最後になるでしょう。2 度と書きたくない 💦
筆者が調べた限りは、資産運用に関するネット上の情報はそのほとんどが思い込みに基づくものであったり、明らかな誤りが含まれていたりと、信頼できる情報は非常に少なかったです。もちろん一部の人は良識あふれる記事を書いていましたが、「普通の人」がそれらを自分で発見して理解して活かすのは難しそうです。
少なくとも筆者が知り合いに安心してオススメできるような、必要な情報を 1 ページにまとめた記事は皆無でした。そのため、筆者の考えをなるべく 1 ページ(?)にまとめて共有することにしました。もともとは知り合いだけに共有するつもりでしたが、公開しました。これで筆者も次からはこの記事の URL (https://hayatoito.github.io/2020/investing/) を教えるだけで済みます。公開するとなにか面倒くさそうなことが起きそうな気がしますが、そのときは非公開にします。
資産運用はサイエンスというよりはエンジニアリングです。ぜひ専門家の方からのフィードバックをお待ちしています (GitHub Issues)。
資産運用は、眠っている資金を市場に送って必要とする人に適切に届けるという行為であり、(間接的に)企業の株を購入し企業活動を応援するという行為です。個人にとっても、企業にとっても、経済にとっても、社会にとっても、Win-Win の関係になれるプラスサムゲームです。
この記事が必要な人に届けば幸いです。