SRM287 に挑戦． 1 ヶ月ぶりの参戦．

TwoEquations (code)

300 点問題．以下のような 2 つの文字列が与えられます．

"1*X + 2*Y = 6"
"1*X + (-4)*Y = (-3)"

連立 2 元方程式です．「中学生か俺は？」でした．．これを解いて，解が唯一存在するならば，以下のように解を文字列で

"X=(-7)/3 Y=3/4"

解がないならば

"NO SOLUTIONS"

を，解が複数存在するならば

"MULTIPLE SOLUTIONS"

を返しなさい．という問題です. 250 点問題ではなく 300 点問題ですのでちょっと面倒です．ですがそれほど難しい問題ではないと一見思ったのですが．．

方針としては，各係数 A1-A3, B1-B3

A1 * X + A2 * Y = A3
B1 * X + B2 * Y = B3

をパースしてから，

int det = A1 * B2 - A2 * B1;
int x = B2 * A3 - A2 * B3;
int y = A1 * B3 - B1 * A3;

を計算して，det == 0 ならば，「解がない」か「解が複数」

if (det == 0) {
    if (x == 0) {
        return "MULTIPLE SOLUTIONS";
    }
    return "NO SOLUTIONS";
}

それ以外ならば，「解がひとつ」ということで，

"X=x/det Y=y/det"

として，約分等・正しくフォーマットして返せばよい．これでいけると思って Submit したのですが，甘かったです．

これだけでは，以下のような係数がゼロの場合に対処できませんでした．

"0*X + 0*Y = 1"
"0*X + 0*Y = 2"

この場合は，正しい正解は"NO SOLUTIONS"ですが，上記ロジックだけだと"MULTIPLE SOLUTIONS"を返してしまいます．

以下のように係数ゼロを特別に扱う必要性がありました．

if (A1 == 0 && A2 == 0 && A3 != 0) return "NO SOLUTIONS";
if (B1 == 0 && B2 == 0 && B3 != 0) return "NO SOLUTIONS";
if (A1 == 0 && B1 == 0 && (A2 * B3 - B2 * A3) != 0) return "NO SOLUTIONS";
if (A2 == 0 && B2 == 0 && (A1 * B3 - B1 * A3) != 0) return "NO SOLUTIONS";

私も含めて多くの人はゼロのケースを考慮しない Code を書いてしまったようです．これに気づいた人は，チャレンジタイムで大稼ぎしていました．

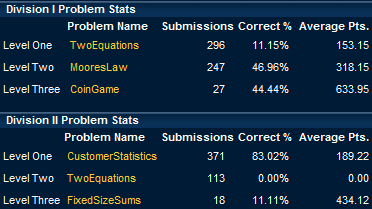
この問題の Division1 での正解率は 11%，同じ問題が Division2 のレベル 2 問題にも使用されていましたが Division2 ではなんと正解率 0%，誰ひとり正解できなかったようです．．

Problem Stats

MooresLaw (code)

450 点問題．

「ムーアの法則」: コンピュータのスピードは，18 ヶ月で 2 倍になる

今，計算を始めると 14 年かかる問題があるとします．今すぐ始めるのではなく，18 ヶ月待ってスピードが 2 倍の新しいコンピュータを買ってそれで計算を始めると 7 年ですみます． 14 年かかる計算が，合計 (1.5 + 7 = ) 8.5 年ですむわけです．この例だと，約 4 年まってから計算を始めるのがベストです．合計( 4 + 2.2 = ) 6.2 年ですみます.

このように，計算にかかる年数 (years) が与えられた場合，ムーアの法則が成り立つとすると，最短・今から何年後に計算を終わらせることができるでしょうか？という問題です．いつ新しいコンピュータを買い計算をはじめるか？がポイントになります．

x 年後に，新しいコンピュータを買って計算を始めるとすると，トータルでは

y = x + (years / 2^(x / 1.5) )

かかることになります．この y が最小になる x を探せばよいことになります．数学的に解くことはできるのでしょうが（微分してゼロになるところを求める）．．数学的に悩むよりは，このような U 字型の関数の場合は，いわゆる binary search ではなく，ternary search で，y が最小になる x を探すことができます．

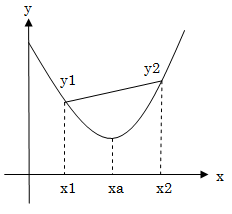
ternary search

区間 ( [left, right] ) 内の 2 点(x1, x2)をとり，y1, y2 を計算して，

y1 > y2 ならば，left = x1
y1 < y2 ならば，right = x2

として，区間を狭めていけば，最終的には，最小の y をとる xa にたどり着きます.

public class MooresLaw {

  public double shortestComputationTime(int years) {

      double left = 0;
      double right = years;

      while (right - left > 1e-11) {
          double x1 = (left * 2 + right) / 3.0;
          double x2 = (left + right * 2) / 3.0;
          if (cal(x1, years) > cal(x2, years)) {
              left = x1;
          } else {
              right = x2;
          }
      }
      return cal(right, years);
  }

  double cal(double x, int years) {
      return x + years / Math.pow(2, x / 1.5);
  }

SRM 中は，x 年後のコンピュータのスピードが，Math.pow(2, x / 1.5) で表せることにきずかず，前半部分・回りくどいことをしていまいました．．．なんとか正解しましたが．

CoinGame

1000 点問題． Open したものの，手が出ず．．

結果

System Test の結果です． ( Room Statistics )

Room Statistics

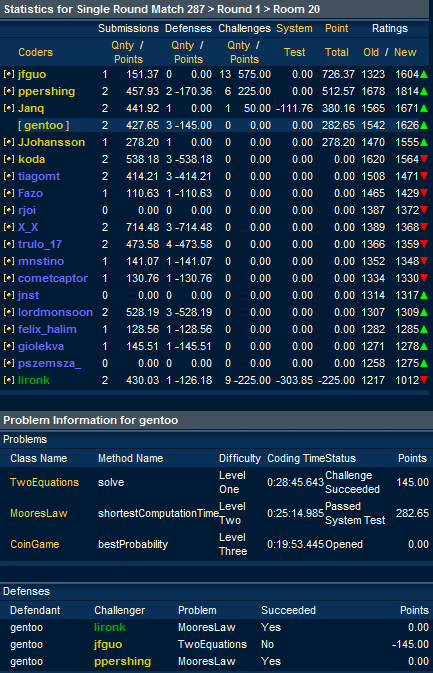
全体的にポイントが低かったためか，レーティングは 1542 -> 1626 と上昇しました．