SRM272 に挑戦．今回の SRM は，msn がスポンサーです．$5,000 の賞金がでます． TopCoder では，ときどきこのような Sponsored Match が行わています．優秀な人材がほしい企業と，名を売りたい人たちの出会いの場の役目も果たしています.

FewestFactors (code)

250 点問題．数字(0〜9)が最大 5 個与えられます．それらを並べ替えてできる最大 5 桁の数のうち，Factor(約数)の数が最も少ないものを求める問題です．たかだか最大 5 個ですので，全ての並び方を試せば OK です．いわゆる permutation です． C++ だと， STL にその名もずばり next_permutation() がありますので，それを使うとよいです． C++以外の言語では，DFS (depth first search)で再帰的に permutation を生成すればよいでしょう．

RoundTable (code)

500 点問題． A 社の代表 (countA)人と B 社の代表 (countB) 人が円卓に座ってミーティングをします．椅子の数は (chairs) です．同じ会社の人どおしは，隣り合って座ってもよいですが， A 社の人と B 社の人は，間に距離をいす(minDistance) 分だけあけて座らなければいけません．

minDistance = 1 は，隣り合っていてもいいです．
minDistance = 2 だと，間に最低 1 つのいすが必要．
minDistance = 3 だと，間に最低 2 つのいすが必要．
...

というわけです．可能な座り方の数はいくつか? という問題です． SRM では，Recursive と Memoization というパターンでときました．この手の問題は，DP(Dynamic Programming:動的計画法)を用いることもできます．こんな感じになります．

public class RoundTable {

  public long arrangements(int countA, int countB, int chairs, int minDis) {
    long[][][][][] dp = new long[chairs][minDis][minDis][countA+1][countB+1];
    dp[0][0][minDis-1][countA-1][countB] = 1;
    for (int c = 1; c < chairs; c++) {
        for (int pa = 0; pa < minDis; pa++) {
            for (int pb = 0; pb < minDis; pb++) {
                for (int a = 0; a <= countA; a++) {
                    for (int b = 0; b <= countB; b++) {
                        int npa = Math.min(minDis-1, pa+1);
                        int npb = Math.min(minDis-1, pb+1);
                        // Neither sit on the chair
                        dp[c][npa][npb][a][b] += dp[c-1][pa][pb][a][b];

                        // Arep can sit on the chair
                        if (pb == minDis-1 && a > 0)
                            dp[c][0][minDis-1][a-1][b] += dp[c-1][pa][pb][a][b] * a;

                        // Brep can sit on the chair
                        if (pa == minDis-1 && b > 0 && c + minDis <= chairs )
                            dp[c][minDis-1][0][a][b-1] += dp[c-1][pa][pb][a][b] * b;
                    }
                }
            }
        }
    }

    long ret = 0;
    for (int pa = 0; pa < minDis; pa++) {
        for (int pb = 0; pb < minDis; pb++) {
            ret += dp[chairs-1][pa][pb][0][0];
        }
    }
    return ret * chairs;
  }
}

レーティングが高い人たちは，平気で DP を使用してきます.

ManhattanDistance

1000 点問題．これも，DP でいけると思ったのですけど，500 点問題で時間をほとんど使いきったため，さすがに時間が足りませんでした. グラフをつくって，Dijkstra 法でもいけます．1000 点問題にしては，とっかかりやすいかと．

結果

System Test の結果です． ( Room Statistics )

Room Statistics

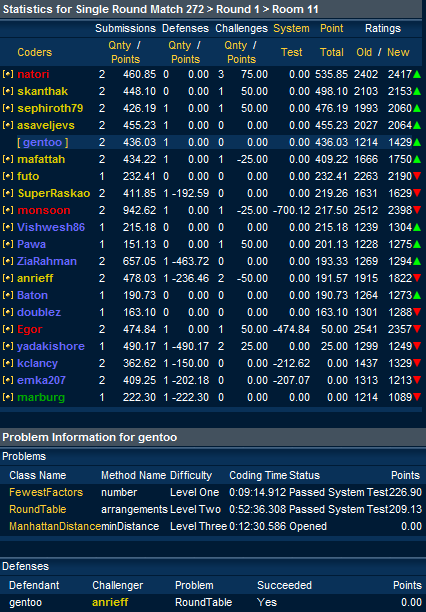
ようやく，Division1 ではじめて System Test に通りました． Level2 問題も解けたので，充実感．レーティングは 1214 -> 1429 と上昇しました．