SRM270 - Integer == Integer

Hayato Ito

SRM270 に挑戦．Division1 に挑戦するのはこれが 3 回目ですが，前の 2 回は，

とまだ 1 問も System Test に通ったことがありません．今度こそは 1 問は通るように．．

CountriesRanklist (code)

300 点問題． Code は提出．今度こそ大丈夫と思っていたもの，また System Test で落ちてしまいました．どこがおかしいんだろと Code を見ていて，5 分ほど．ようやく間違いを発見しました．ここです

if (l.get(i) == maxscore.get(key))

Integer と Integer を == で比較しています．．．あーやってしまった． J2SE5 から autoboxing/unboxing が使えるようになりましたが，すっかりそれに頼りきっていました．このように左辺 と 右辺 ともに Integer の場合は，だめですね．．equals(..) じゃないと． どちらかが int ならよかったんだけど．また単純ミスだ．．

SalesmanDilemma

600 点問題． 巡回セールスマン問題．．ではありません．基本的には最短経路を求める問題に落ち着くのですが，やっかいな点としてネガティブ・ループの考慮をする必要があります． SRM 中は，時間切れで Submit できませんでした．もう少しだったんですけど．

SRM 後に，完成させたコードです．タイムオーバーになるかと思ったのですが，今回の条件ではこれでも十分 2 秒以内でした．

import java.util.Scanner;
public class SalesmansDilemma {

int[][] p;
int[] visited;
int destination;

final int NA = Integer.MIN_VALUE;
final int ENDLESS = Integer.MAX_VALUE;
final int IMPOSSIBLE = Integer.MIN_VALUE;

int goal = IMPOSSIBLE;

public String bestRoute(int towns, int origin, int destination,
        String[] travelCosts, int[] profits) {
    this.destination = destination;
    p = new int[towns][towns];
    for (int i = 0; i < towns; i++) Arrays.fill(p[i], NA);
    for (int i = 0; i < travelCosts.length; i++) {
        Scanner s = new Scanner(travelCosts[i]);
        int from = s.nextInt();
        int to = s.nextInt();
        int cost = s.nextInt();
        p[from][to] = Math.max(p[from][to], profits[to] - cost);
    }

    visited = new int[towns];
    Arrays.fill(visited, IMPOSSIBLE);
    visited[origin] = 0;
    go(origin);

    if (goal == IMPOSSIBLE) return "IMPOSSIBLE";
    if (goal == ENDLESS) return "ENDLESS PROFIT";
    return "BEST PROFIT: " + (goal + profits[origin]);
}

void go(int town) {
    if (town == destination) goal = Math.max(goal, visited[town]);

    for (int i = 0; i < p[town].length; i++) {
        if (p[town][i] == NA) continue;

        int old = visited[i];
        int update = (visited[town] == ENDLESS) ?
                     ENDLESS : visited[town] + p[town][i];

        if (old == IMPOSSIBLE) {
            visited[i] = update;
            go(i);
            visited[i] = old;
        } else if (update > old) {
            visited[i] = ENDLESS;
            go(i);
            visited[i] = old;
        }
    }
}

この手の問題では，Bellman-Ford アルゴリズムを用いるのが定石のようです．ある地点からある地点までの，最短経路，およびネガティブ・ループを発見するアルゴリズムです．練習がてら，Java で実装してみました．

import java.util.Scanner;
public class SalesmansDilemma {

class Edge {
    int source;
    int destination;
    int weight;
}

public String bestRoute(int towns, int origin, int destination,
        String[] travelCosts, int[] profits) {
    Edge[] edges  = new Edge[travelCosts.length];
    for (int i = 0; i < travelCosts.length; i++) {
        Scanner scan  = new Scanner(travelCosts[i]);
        edges[i] = new Edge();
        edges[i].source = scan.nextInt();
        edges[i].destination = scan.nextInt();
        edges[i].weight = scan.nextInt()
                         - profits[edges[i].destination];
    }
    long[] verticles = new long[towns];
    long INFINITY = Long.MAX_VALUE;
    for (int i = 0; i < verticles.length; i++) {
        verticles[i] = INFINITY;
    }
    verticles[origin] = 0;

    boolean[] negative = new boolean[towns];

    // relax and find negative cycle
    for (int i = 0; i < verticles.length + 1; i++) {
        for (Edge e : edges) {
            int u = e.source;
            int v = e.destination;
            if (verticles[u] == INFINITY) continue;
            if (verticles[v] > verticles[u] + e.weight) {
                verticles[v] = verticles[u] + e.weight;
                if (i == verticles.length) {
                    negative[v] = true;
                }
            }
        }
    }

    if (verticles[destination] == INFINITY) return "IMPOSSIBLE";

    boolean[] mark = new boolean[towns];
    for (int i = 0; i < towns; i++) {
        if (negative[i] && !mark[i]) {
            go(i, mark, edges);
        }
    }
    if (mark[destination]) return "ENDLESS PROFIT";

    return "BEST PROFIT: " +
           -(verticles[destination] - profits[origin]);
}

void go(int v, boolean[] mark, Edge[] edges) {
    mark[v] = true;
    for (Edge e : edges) {
        if (v == e.source && !mark[e.destination]) {
            go(e.destination, mark, edges);
        }
    }
}
}

PackingShapes

900 点問題． SRM 中は Open しませんでした．ある長方形のなかに，別の長方形をはみださないようにいれることができるか判定する問題です．たとえば，幅 100 x 高さ 100 の長方形には，幅 140 x 高さ 1 の長方形は（傾ければ）いれることができます． 幅 140 x 50 の長方形はどんなにがんばってもはいりません．

結果

System Test の結果です． ( Room Statistics )

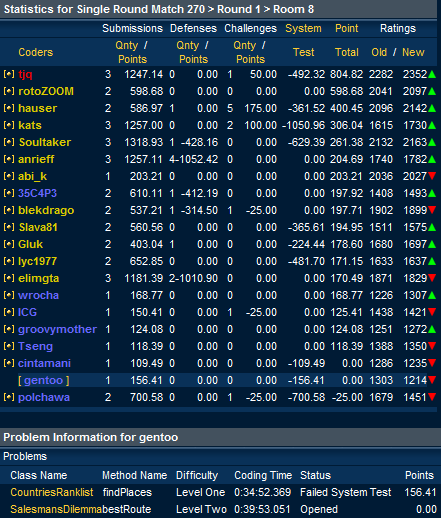
Room Statistics

レーティングは 1303 -> 1214 と低下．かろうじて Division1 には残っています.

今日の教訓